K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 7 2021
a) Để y nguyên thì \(6x-4⋮2x+3\)
\(\Leftrightarrow-13⋮2x+3\)
\(\Leftrightarrow2x+3\in\left\{1;-1;13;-13\right\}\)
\(\Leftrightarrow2x\in\left\{-2;-4;10;-16\right\}\)
hay \(x\in\left\{-1;-2;5;-8\right\}\)
LH
1
18 tháng 7 2021
b) Ta quy đồng rồi => x+xy = 4
=> x(y+1) = 4 thì 1/x−y/2=1/4
NT
0
ZD
9 tháng 7 2017
Viết lại thành : \(\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}\)
Dựa theo tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x+y+z}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{49}{\dfrac{49}{12}}=12\)
-> x = \(12.\dfrac{3}{2}=18\)
y =\(12.\dfrac{4}{3}=16\)
z =\(12.\dfrac{5}{4}\) = 15
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
\(y=\dfrac{2\left(2x+5\right)-18}{2x+5}=2-\dfrac{18}{2x+5}\)
\(y\in Z\Rightarrow\dfrac{18}{2x+5}\in Z\Rightarrow2x+5=Ư\left(18\right)\)
Mà 2x+5 luôn lẻ nên ta có: \(2x+5=\left\{-9;-3;-1;1;3;9\right\}\)
| 2x+5 | -9 | -3 | -1 | 1 | 3 | 9 |
| x | -7 | -4 | -3 | -2 | -1 | 2 |
| y | 4 | 8 | 20 | -16 | -4 | 0 |
AH
Akai Haruma
Giáo viên
23 tháng 7 2023
Lời giải:
$3x-2y+6xy=1$
$\Rightarrow (3x+6xy)-(2y+1)=0$
$\Rightarrow 3x(1+2y)-(2y+1)=0$
$\Rightarrow (1+2y)(3x-1)=0$
$\Rightarrow 1+2y=0$ hoặc $3x-1=0$
$\Rightarrow y=\frac{-1}{2}$ hoặc $x=\frac{-1}{3}$ (vô lý vì $x,y$ là số nguyên)
Vậy không tồn tại $x,y$ thỏa mãn đề.
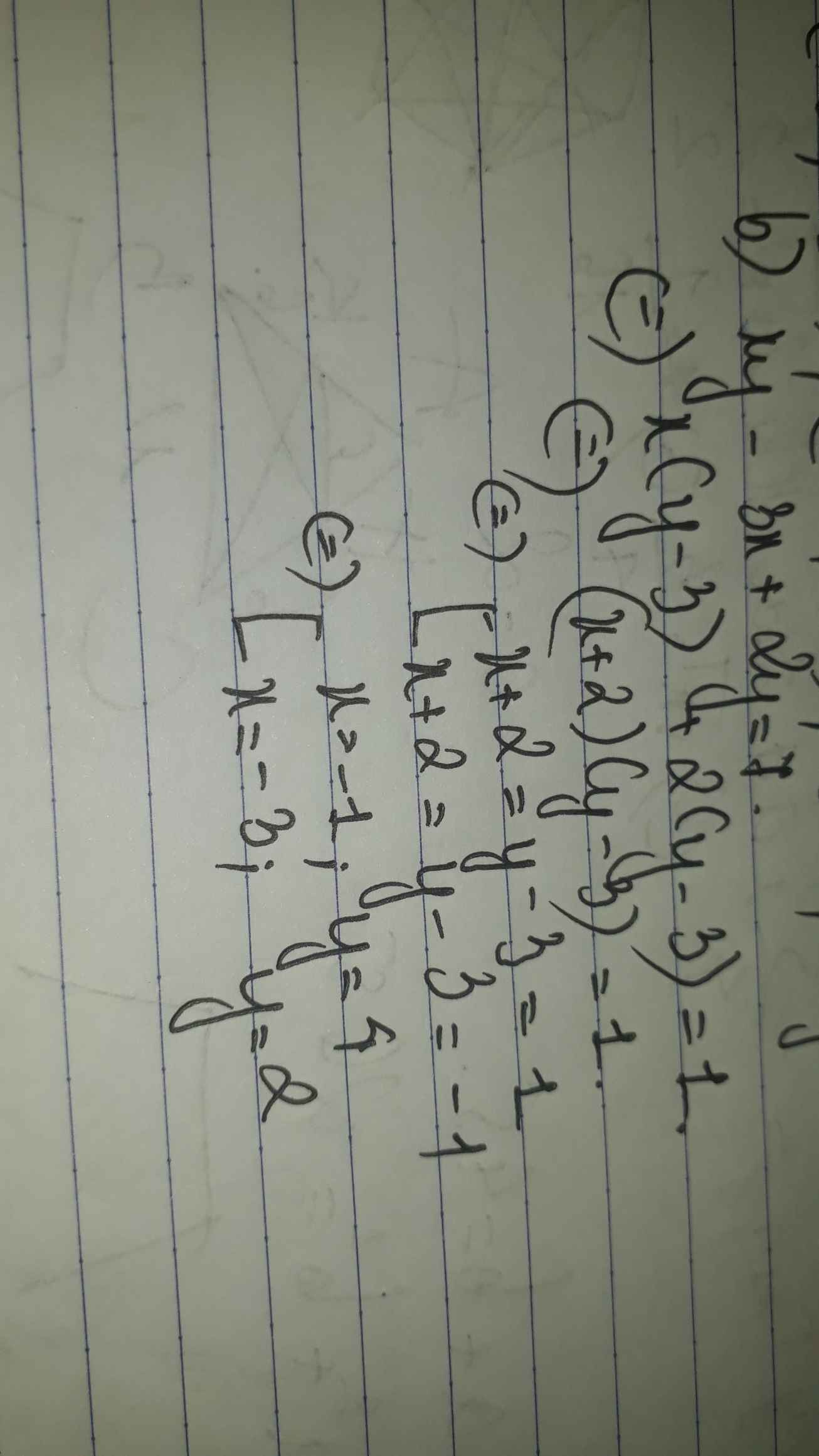
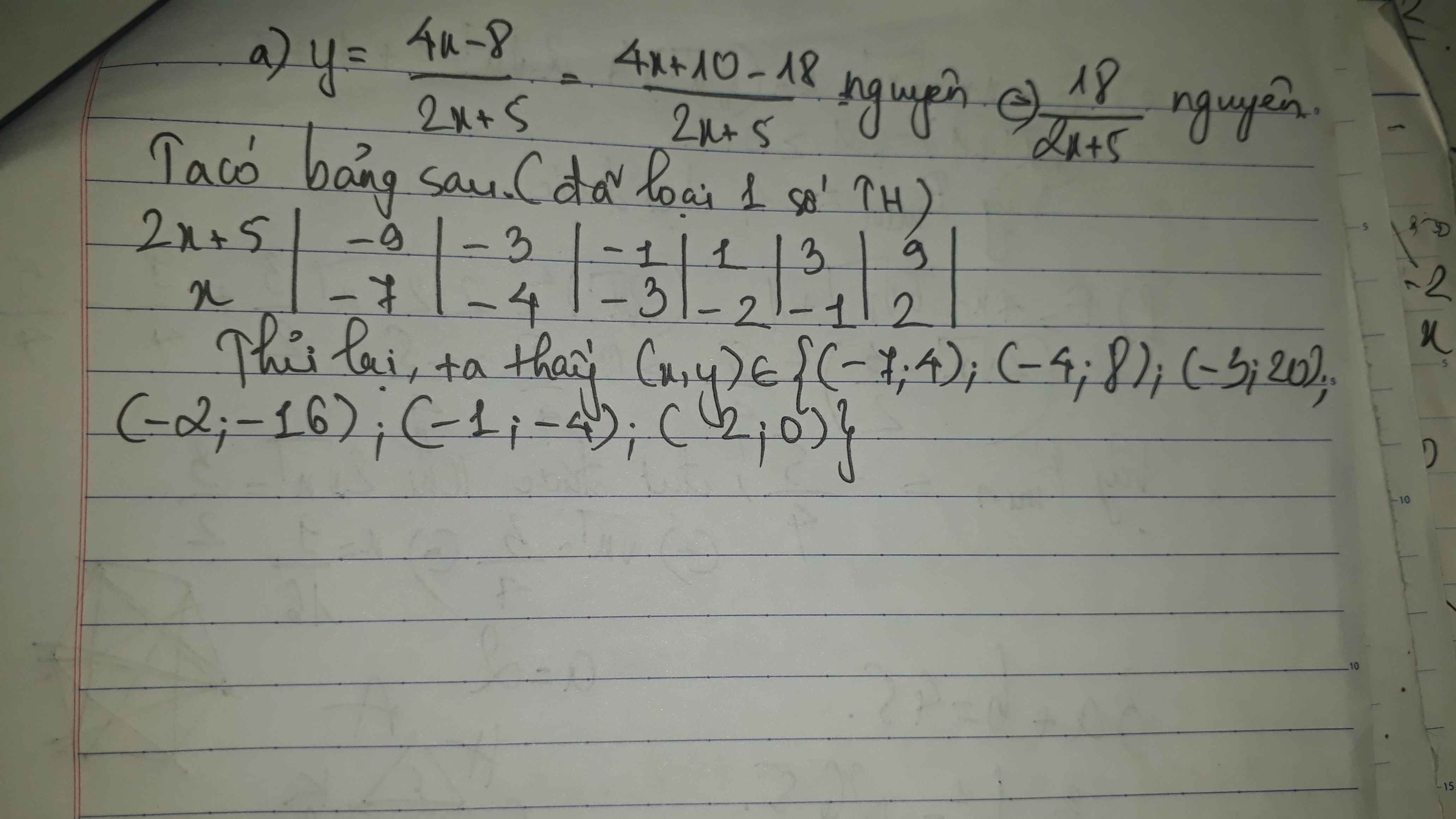
\(\left(3x-5\right)\left(2x+1\right)=12\)
\(\Rightarrow3x-5;2x+1\inƯ\left(12\right)=\left\{\pm1;\pm2;\pm3;\pm4;\pm6;\pm12\right\}\)
Vậy x = 3 ; y = 1
Có (3x-5)(2x+1)=12
Vì x thuộc Z mà (3x-5)(2x+1)=12
=>(3x-5 , 2x+1) thuộc Ư(12)={1;2;3;4;6;12;-1;-2;-3;-4;-6;-12}
Có x thuộc Z =>2x+1 lẻ
=>2x+1 thuộc {1;3;-1;-3}
Ta có bảng sau:
Còn lại bn tự lm nha