NN
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 3 2020
\(a,2x+1⋮x-2\)
\(=>2.\left(x-2\right)+5⋮x-2\)
Do \(2.\left(x-2\right)⋮x-2\)
\(=>5⋮x-2\)
\(=>x-2\inƯ\left(5\right)\)
Nên ta có bảng sau :
| x-2 | 1 | 5 | -1 | -5 |
| x | 3 | 7 | 1 | -3 |
Vậy ...
\(b,3x+5⋮x\)
Do \(3x⋮x=>5⋮x\)
\(=>x\inƯ\left(5\right)\)
Nên ta có bảng sau :
| x | 1 | 5 | -1 | -5 |
Vậy ...
\(c,4x+1⋮2x+3\)
\(=>2.\left(2x+3\right)-5⋮2x+3\)
Do \(2.\left(2x+3\right)⋮2x+3\)
\(=>5⋮2x+3\)
\(=>2x+3\inƯ\left(5\right)\)
Nên ta có bảng sau :
| 2x+3 | 1 | 5 | -1 | -5 |
| 2x | -2 | 2 | -4 | -8 |
| x | -1 | 1 | -2 | -4 |
Vậy ...
6 tháng 3 2020
a) Ta có: 2x+1=2(x-2)+5
Để 2x+1 chia hết cho x-2 thì 2(x-2)+5 chia hết cho x-2
Vì 2(x-2) chia hết cho x-2
=> 5 chia hết cho x-2
Vì x thuộc Z => z-2 thuộc Ư (5)={-5;-1;1;5}
Nếu x-2=-5 => x=-3
Nếu x-2=-1 => x=1
Nếu x-2=1 => x=3
Nếu x-1=5 => x=6
b) Ta có 3x chia hết cho x với mọi x
=> Để 3x+5 chia hết cho x thì 5 chia hết cho x
Vì x thuộc Z => x thuộc Ư (5)={-5;-1;1;5}
c) Ta có: 4x+11=2(2x+3)+5
Để 4x+11 chia hết cho 2x+3 thì 2(2x+3)+5 chia hết cho 2x+3
Vì 2(2x+3) chia hết cho 2x+3 => 5 chia hết cho 2x+3
Vì x thuộc Z => 2x+3 thuộc Ư (5)={-5;-1;1;5}
Nếu 2x+3=-5 => 2x=-8 => x=-4
Nếu 2x+3=-1 => 2x=-4 => x=-2
Nếu 2x+3=1 => 2x=-2 => x=-1
Nếu 2x+3=5 => 2x=2 => x=1
NP
0
S
16 tháng 2 2019
4n+3 chia hết cho 3n-2
<=> 3(4n+3)-4(3n-2) chia hết cho 3n-2
<=>17 chia hết cho 3n-2
<=>3n-2 E {-1;1;17;-17}
<=> 3n E {1;3;19;-15} loại các TH n ko nguyên
=>n E {1;-5}. Vậy.....
29 tháng 10 2017
a, Ta có: x+6 chia hết cho x
=> x chia hết cho x
<=> x e Ư(6) = { 1;2;3;6}
+, Nếu x + 6 = 1
<=> x = 5
+, Nếu x + 6 = 2
<=> x = 4
+, Nếu x + 6 = 3
<=> x = 3
+, Nếu x+6 = 6
<=> x = 0
Vậy x e { 5;4;3}
BD
21 tháng 10 2017
a ) 2x + 5 chia hết cho x + 1
2x + 2 + 3 chia hết cho x + 1
( 2x + 2 ) + 3 chia hết cho x + 1
2x + 2 chia hết cho x + 1 với mọi x . Vậy 3 chia hết cho x + 1
=> x + 1 thuộc Ư( 3)
=> x + 1 thuộc { 1 ; 3 }
Với x + 1 = 1
x = 1 - 1
x = 0
Với x + 1 = 3
x = 3 - 1
x = 2
Vậy x thuộc { 0 ; 2 }
b ) 3x + 15 chia hết cho x + 2
3x + 6 + 9 chia hết cho x + 2
( 3x + 6 ) + 9 chia hết cho x + 2
3x + 6 chia hết cho x + 2 với mọi x . Vậy 9 chia hết cho x + 2
=> x + 2 thuộc Ư( 9 )
=> x + 2 thuộc { 1 ; 3 ; 9 }
Với x + 2 = 1
x = 1 - 2 ( loại )
Với x + 2 = 3
x = 3 - 2
x = 1
Với x + 2 = 9
x = 9 - 2
x = 7
Vậy x thuộc { 1 ; 7 }
c ) 4x + 22 chia hết cho 2x - 1
4x - 2 + 24 chia hết cho 2x - 1
4x - 2 chia hết cho 2x - 1 với mọi x . Vậy 24 chia hết cho 2x - 1
=> 2x - 1 thuộc Ư(24)
=> 2x - 1 thuộc { 1 ; 2 ; 3 ; 4 ; 6 ; 8 ; 12 ; 24 )
Với 2x - 1 = 1
2x = 1 + 1
2x = 2
x = 2 : 2
x = 1
....
Với 2x - 1 = 24
2x = 24 + 1
2x = 25
x = 25 : 2 ( loại )
Vậy x thuộc { 1 ; 2 }
LH
2 tháng 9 2016
đề sai hay sao ấy bn ạ, mình sẽ phân tích cho bn xem nhá
4x + 11 = (3x + 1) + (x + 10)
3x + 1 chia hết cho 3x + 1
vậy x + 10 phải chia hết cho 3x + 1
mà bn thấy nhé, x và 10 phải chia hết 3x + 1
mà x đã ko chia hết cho 3x + 1 nhá, nên mình nghĩ là đề sai đấy bn ạ, nếu mình sai thì để mình tính lại, có thể mình hoặc đề sai, mình sẽ xem lại bn nhá
NT
0
26 tháng 1 2016
kho..................lam............................tich,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,minh..........................troi........................ret............................wa.................ung ho minh.................hu....................hu..............hu................hat..............hat....................s
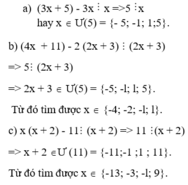
Ta có: \(\frac{3x+5}{3x+1}=\frac{3x+1+4}{3x+1}=1+\frac{4}{3x+1}\)
Để \(\left(3x+5\right)⋮\left(3x+1\right)\)thì \(4⋮3x+1\)
\(\Rightarrow3x+1\inƯ\left(4\right)\)
\(\Rightarrow3x+1\in\left\{1;2;4;-1;-2;-4\right\}\)
\(\Rightarrow3x\in\left\{0;1;3;-2;-3;-5\right\}\)
\(\Rightarrow x\in\left\{0;\frac{1}{3};1;-\frac{2}{3};-1;-\frac{5}{3}\right\}\)
Mà \(x\in N\Rightarrow x\in\left\{0;1;-1\right\}\)
b, Ta có: \(\frac{4x+11}{x-3}=\frac{4x-12+23}{x-3}=\frac{4\left(x-3\right)+23}{x-3}=4+\frac{23}{x-3}\)
Để \(\left(4x+11\right)⋮\left(x-3\right)\)thì \(23⋮x-3\)
\(\Rightarrow x-3\inƯ\left(23\right)\)
\(\Rightarrow x-3\in\left\{1;23;-1;-23\right\}\)
\(\Rightarrow x\in\left\{4;26;2;-20\right\}\)
Mà \(x\in N\Rightarrow x\in\left\{4;26;2\right\}\)
a) 3x+5 chia hết cho 3x+1
=> 3x+1+4 chia hết cho 3x+1
=> (3x+1)+4 chia hết cho 3x+1
=> 3x+1 chia hết cho 3x+1 ; 4 chia hết cho 3x+1
=> 3x+1 thuộc Ư(4)={1,2,4}
=> x thuộc {0,1} (thõa mãn đk thuộc N)
b) 4x+11 chia hết cho x-3
=> 4x-12+23 chia hết cho x-3
=> 4(x-3)+23 chia hết cho x-3
=> 4(x-3) chia hết cho x-3 ; 23 chia hết cho x-3
=> x-3 thuộc Ư(23)={1,23}
=> x thuộc {4,26} ( thõa mãn đk thuộc N)