K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
GN
7
N
22 tháng 10 2018
\(x^3-11x^2+30x=0\)
\(\left(x-6\right).\left(x-5\right).x=0\)
\(=>\orbr{\begin{cases}x-6=0\\x-5=0,x=0\end{cases}}\)
\(=>\orbr{\begin{cases}x=6\\x=5,x=0\end{cases}}\)
P/S: mk mới lớp 7 sai sót mong bỏ qua
N
22 tháng 10 2018
\(8x^2+30x+7=0\)
\(8x^2+28x+2x+7=0\)
\(2x.\left(4x+1\right)+7.\left(4x+1\right)=0\)
\(\left(2x+7\right).\left(4x+1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}2x=-7\\4x=-1\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=-\frac{7}{2}\\x=-\frac{1}{4}\end{cases}}\)
vậy ....
P/S sorry mk làm hơi lâu :)__chờ tí làm câu a cho
BC
1
16 tháng 10 2018
b) 8x2 + 30x + 7 = 0
8x2 + 16x + 14x + 7 = 0
8x.(x+2) + 7.(x+2) = 0
(x+2).(8x+7) = 0
..
bn tự làm tiếp nhé! ^-^
c) x3 - 11x2 + 30x = 0
x.(x2 - 11x +30) = 0
\(x.\left(x^2-5x-6x+30\right)=0.\)
x.[ x.(x-5) - 6.(x-5) ] = 0
x.(x-5).(x-6) = 0
...
MK
2
21 tháng 7 2016
\(x^2+3x-18=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+6\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\\x+6=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=3\\x=-6\end{cases}}}\)
\(8x^2+30x+7=0\)
\(\Leftrightarrow\left(x+\frac{1}{4}\right)\left(x+\frac{7}{2}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+\frac{1}{4}=0\\x+\frac{7}{2}=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{-1}{4}\\x=-\frac{7}{2}\end{cases}}}\)
\(x^3-11x^2+30x=0\)
\(\Leftrightarrow x\left(x-6\right)\left(x-5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-6=0\\x-5=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=6\\x=5\end{cases}}}\)hoặc \(x=0\)
21 tháng 7 2016
\(x^2+3x-18=x^2-3x+6x-18=x\left(x-3\right)+6\left(x-3\right)=\left(x-2\right)\left(x+6\right)\)
9 tháng 12 2018
\(x^4-30x^2+31x-30=0\)
\(\left(x^4+x\right)-30\left(x^2-x+1\right)=0\)
\(x\left(x^3+1\right)-30\left(x^2-x+1\right)=0\)
\(x\left(x+1\right)\left(x^2-x+1\right)-30\left(x^2-x+1\right)=0\)
\(\left(x^2-x+1\right)\left[x\left(x+1\right)-30\right]=0\)
Ta có: \(x^2-x+1=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\)
\(\Rightarrow x^2+x-30=0\left(x^2-x+1\ne0\right)\)
\(\left(x^2-5x\right)+\left(6x-30\right)=0\)
\(x\left(x-5\right)+6\left(x-5\right)=0\)
\(\left(x-5\right)\left(x+6\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-5=0\\x+6=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=5\\x=-6\end{cases}}}\)
Vậy \(\orbr{\begin{cases}x=5\\x=-6\end{cases}}\)
31 tháng 7 2017
a,\(15x^3y^4-20x^4y^3+30x^3y^3\)
=\(5x^3y^3\left(3y-4x+6\right)\)
b,\(x^2+10xy+25y^2\)
=\(x^2+2.x.5.y+\left(5y\right)^2\)
=\(\left(x+5y\right)^2\)
c,\(x^2-2xy+y^2-9z^2\)
=\(\left(x^2-2xy+y^2\right)-\left(3z\right)^2\)
=\(\left(x-y\right)^2-\left(3z\right)^2\)
=\(\left(x-y+3z\right)\left(x-y-3z\right)\)
chúc bn hok tốt 
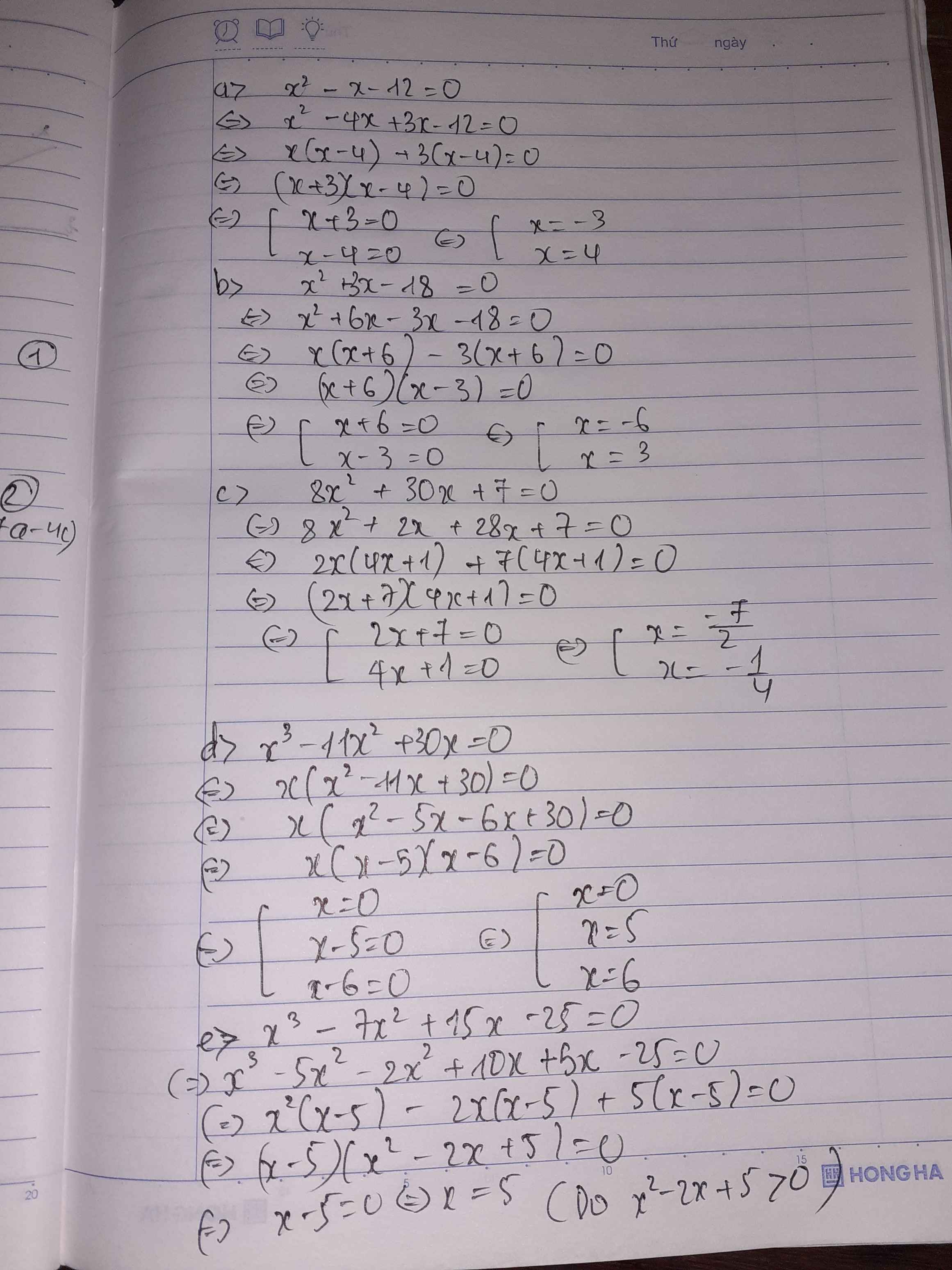
\(30x-15x^2-0\)
\(\Leftrightarrow15x\left(2-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}15x=0\\2-x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)