Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\sqrt{4x^2}=6\Rightarrow\left|2x\right|=6\Rightarrow\left[{}\begin{matrix}2x=6\\2x=-6\end{matrix}\right.\) \(\Rightarrow x=\pm3\)
b/ ĐKXĐ: \(x\ge0\)
\(\sqrt{16x}=8\Leftrightarrow16x=64\Rightarrow x=4\)
c/ ĐKXĐ: \(x\ge1\)
\(\sqrt{9\left(x-1\right)}=21\Leftrightarrow\sqrt{x-1}=7\Leftrightarrow x-1=49\Rightarrow x=50\)
d/ \(\sqrt{4\left(1-x\right)^2}=6\Leftrightarrow2\left|1-x\right|=6\Leftrightarrow\left|1-x\right|=3\Rightarrow\left[{}\begin{matrix}x=-2\\x=4\end{matrix}\right.\)
e/ \(\sqrt{1-4x+4x^2}=5\Leftrightarrow\sqrt{\left(2x-1\right)^2}=5\Leftrightarrow\left[{}\begin{matrix}2x-1=5\\2x-1=-5\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)
f/ĐKXĐ: \(x\ge-\frac{1}{2}\)
\(\sqrt{9x^2}=2x+1\Leftrightarrow\left|3x\right|=2x+1\Leftrightarrow\left[{}\begin{matrix}3x=2x+1\\-3x=2x+1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=-\frac{1}{5}\end{matrix}\right.\)

\(f,\sqrt{x^2-25}-\sqrt{x-5}=0\)
=> \(\sqrt{x^2-25}=\sqrt{x-5}\)
=>\(x^2-25=x-5\)
=>\(x^2-x=25-5=20\)
=>( đến đoạn này mình xin chịu )
\(a,\sqrt{16x}=8\)
=>\(16x=8^2\)
=>\(16x=64\)
=>\(x=64:16=4\)
Vậy \(x\in\left\{4\right\}\)
\(b,\sqrt{x^2}=2x-1\)
=>\(x=2x-1\)
=>\(2x-x=1\)
=>\(x=1\)
Vậy \(x\in\left\{1\right\}\)
\(c,\sqrt{9.\left(x-1\right)}=21\)
=>\(9.\left(x-1\right)=21^2=441\)
=> \(x-1=441:9=49\)
=>\(x=49+1=50\)
Vậy \(x\in\left\{50\right\}\)
\(d,\sqrt{4\left(1-x\right)^2}-6=0\)
=>\(\sqrt{4\left(1-x\right)^2}=0+6=6\)
=> \(4\left(1-x\right)^2=6^2=36\)
=>\(\left(1-x\right)^2=36:4=9\)
=>\(1-x=\sqrt{9}=3\)
=>\(x=1-3=-2\)
Vậy \(x\in\left\{-2\right\}\)
\(g,\sqrt{9\left(2-3x\right)^2}=6\)
=> \(9.\left(2-3x\right)^2=6^2=36\)
=> \(\left(2-3x\right)^2=36:9=4\)
=> \(2-3x=\sqrt{4}=2\)
=>\(3x=2-2=0\)
=>\(x=0:3=0\)
Vậy \(x\in\left\{0\right\}\)
( còn các bài còn lại mình sẽ nghĩ tiếp , HS6-7 làm bài )

Mình làm một vài câu thôi nhé, các câu còn lại tương tự.
Giải:
a) ??? Đề thiếu
b) \(\sqrt{-3x+4}=12\)
\(\Leftrightarrow-3x+4=144\)
\(\Leftrightarrow-3x=140\)
\(\Leftrightarrow x=\dfrac{-140}{3}\)
Vậy ...
c), d), g), h), i), p), q), v), a') Tương tự b)
w), x) Mình đã làm ở đây:
Câu hỏi của Ami Yên - Toán lớp 9 | Học trực tuyến
z) \(\sqrt{16\left(x+1\right)^2}-\sqrt{9\left(x+1\right)^2}=4\)
\(\Leftrightarrow4\left(x+1\right)-3\left(x+1\right)=4\)
\(\Leftrightarrow x+1=4\)
\(\Leftrightarrow x=3\)
Vậy ...
b') \(\sqrt{9x+9}+\sqrt{4x+4}=\sqrt{x+1}\)
\(\Leftrightarrow3\sqrt{x+1}+2\sqrt{x+1}=\sqrt{x+1}\)
\(\Leftrightarrow3\sqrt{x+1}+2\sqrt{x+1}-\sqrt{x+1}=0\)
\(\Leftrightarrow4\sqrt{x+1}=0\)
\(\Leftrightarrow x+1=0\)
\(\Leftrightarrow x=-1\)
Vậy ...
- Câu a có chút thiếu sót, mong thông cảm :)
\(\sqrt{3x-1}\) = 4

\(\sqrt{\left(\sqrt{3}+1\right)^2}+\sqrt{\left(\sqrt{3}-1\right)^2}+\frac{5\left(2\sqrt{2}+\sqrt{3}\right)}{\left(2\sqrt{2}+\sqrt{3}\right)\left(2\sqrt{2}-\sqrt{3}\right)}-\frac{5\left(\sqrt{8}-\sqrt{3}\right)}{\left(\sqrt{8}-\sqrt{3}\right)\left(\sqrt{8}+\sqrt{3}\right)}\)
\(=\sqrt{3}+1+\sqrt{3}-1+\frac{5\left(2\sqrt{2}+\sqrt{3}\right)}{5}-\frac{5\left(\sqrt{8}-\sqrt{3}\right)}{5}\)
\(=2\sqrt{3}+2\sqrt{2}+\sqrt{3}-\sqrt{8}+\sqrt{3}\)
\(=4\sqrt{3}\)
Giải pt:
1/ \(\Leftrightarrow2x-1=5\)
\(\Leftrightarrow2x=6\Rightarrow x=3\)
2/ \(\Leftrightarrow\sqrt{3}x^2=\sqrt{12}\Leftrightarrow x^2=\sqrt{4}=2\)
\(\Leftrightarrow x=\pm\sqrt{2}\)
3/ \(\Leftrightarrow x-5=9\Rightarrow x=14\)
4/ Đề thiếu
5/ \(\Leftrightarrow\left|x-3\right|=9\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=9\\x-3=-9\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=12\\x=-6\end{matrix}\right.\)
6/ \(\Leftrightarrow2\left|1-x\right|=6\)
\(\Leftrightarrow\left|1-x\right|=3\Leftrightarrow\left[{}\begin{matrix}1-x=3\\1-x=-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=4\end{matrix}\right.\)
7/ \(\Leftrightarrow9\left(x-1\right)=21^2\)
\(\Leftrightarrow x-1=49\Rightarrow x=50\)
8/ \(\Leftrightarrow x+1=2^3=8\)
\(\Rightarrow x=7\)
9/ \(\Leftrightarrow\sqrt{\left(2x+1\right)^2}=6\Leftrightarrow\left|2x+1\right|=6\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=6\\2x+1=-6\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\frac{5}{2}\\x=-\frac{7}{2}\end{matrix}\right.\)
10/ \(\Leftrightarrow\sqrt{2}x=\sqrt{50}\Leftrightarrow x=\sqrt{25}\Rightarrow x=5\)
11/ \(\Leftrightarrow\left|2x-1\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=3\\2x-1=-3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
12/ \(\Leftrightarrow3-2x=\left(-2\right)^3=-8\)
\(\Leftrightarrow2x=11\Rightarrow x=\frac{11}{2}\)

Hung nguyen, Trần Thanh Phương, Sky SơnTùng, @tth_new, @Nguyễn Việt Lâm, @Akai Haruma, @No choice teen
help me, pleaseee
Cần gấp lắm ạ!

Ta có \(a,\sqrt{9(x-1)}=21 \)
<=> \(3\sqrt{x-1}=21 \)
<=> \(\sqrt{x-1}=7 \)
<=>\(x-1=49\)
<=>x=50
b, \(\sqrt{4(x-1)^2}-6=0 \)
<=>\(2|x-1|-6=0\)
<=>\(|x-1|=3\)
<=>x=4 hoặc x=-2
c,\(\sqrt{(x-5)^2}=8 \)
<=>|x-5|=8
<=>x=-3 hoặc x=13
d,\(\sqrt{(2x-1)^2}=3 \)
<=>|2x-1|=3
=> x=2 hoặc x=-1
e, \(\sqrt{(2x+3)^2}=3 \)
<=>|2x+3|=3
=>x=0 hoặc x=-3
f, \(\sqrt{x^2-4x+4}=2x-3 \)
<=>\(\sqrt{(x-2)^2}=2x-3 \)
<=>|x-2|=2x-3
Với x-2=2x-3
=>x-1=0
<=>x=1
Với 2-x=2x-3
=>x=\(\frac{5}{3}\)

bài 1:
a)\(\left(3-\sqrt{2}\right)\sqrt{7+4\sqrt{3}}\)
\(=\left(3-\sqrt{2}\right)\sqrt{\left(2+\sqrt{3}\right)^2}\)
\(=\left(3-\sqrt{2}\right)\left(2+\sqrt{3}\right)\)\(do2>\sqrt{3}\)
\(=6+3\sqrt{3}-2\sqrt{2}-\sqrt{6}\)
b) \(\left(\sqrt{3}+\sqrt{5}\right)\sqrt{7-2\sqrt{10}}\)
\(=\left(\sqrt{3}+\sqrt{5}\right)\sqrt{\left(\sqrt{5}-\sqrt{2}\right)^2}\)
\(=\left(\sqrt{3}+\sqrt{5}\right)\left(\sqrt{5}-\sqrt{2}\right)do\sqrt{5}>\sqrt{2}\)
\(=\sqrt{15}-\sqrt{6}+5-\sqrt{10}\)
c)\(\left(2+\sqrt{5}\right)\sqrt{9-4\sqrt{5}}\)
\(=\left(2+\sqrt{5}\right)\sqrt{\left(\sqrt{5}-2\right)^2}\)
\(=\left(2+\sqrt{5}\right)\left(\sqrt{5}-2\right)do\sqrt{5}>2\)
\(=5-4\)
\(=1\left(hđt.3\right)\)
d)\(\left(\sqrt{6}+\sqrt{10}\right)\sqrt{4-\sqrt{15}}\)
\(=\sqrt{2}\left(\sqrt{3}+\sqrt{5}\right)\sqrt{4-\sqrt{15}}\)
\(=\left(\sqrt{3}+\sqrt{5}\right)\sqrt{8-2\sqrt{15}}\)
\(=\left(\sqrt{3}+\sqrt{5}\right)\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\)
\(=\left(\sqrt{3}+\sqrt{5}\right)\left(\sqrt{5}-\sqrt{3}\right)do\sqrt{5}>\sqrt{3}\)
\(=5-3\)
\(=2\)
e)\(\sqrt{2}\left(\sqrt{8}-\sqrt{32}+3\sqrt{18}\right)\)
\(=\sqrt{2}\left(2\sqrt{2}-4\sqrt{2}+9\sqrt{2}\right)\)
\(=2\left(2-4+9\right)\)
\(=2.7=14\)
f)\(\sqrt{2}\left(\sqrt{2}-\sqrt{3-\sqrt{5}}\right)\)
\(=2-\sqrt{6-2\sqrt{5}}\)
\(=2-\sqrt{\left(\sqrt{5}-1\right)^2}\)
\(=2-\left(\sqrt{5}-1\right)\)
\(=2-\sqrt{5}+1\)
\(=3-\sqrt{5}\)
g)\(\sqrt{3}-\sqrt{2}\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}\)
\(=\sqrt{3}-\sqrt{2}\left(\sqrt{3}+\sqrt{2}\right)\)
\(=\sqrt{3}-\sqrt{6}-2\)
h) \(\left(\sqrt{2}-\sqrt{3+\sqrt{5}}\right)\sqrt{2}+2\sqrt{5}\)
\(=\left(2-\sqrt{6+2\sqrt{5}}\right)+2\sqrt{5}\)
\(=\left(2-\sqrt{\left(\sqrt{5}+1\right)^2}\right)+2\sqrt{5}\)
\(=2-\left(\sqrt{5}+1\right)+2\sqrt{5}\left(do\sqrt{5}>1\right)\)
\(=2-\sqrt{5}-1+2\sqrt{5}\)
\(=1-\sqrt{5}\)
bài 2)
a) \(\sqrt{4x^2-4x+1}=5\)
\(\Leftrightarrow\sqrt{\left(2x-1\right)^2}=5\)
\(\Leftrightarrow2x-1=5\)hoặc \(\Leftrightarrow2x-1=-5\)
\(\Leftrightarrow x=3\)hoặc \(\Leftrightarrow x=-2\)
Vậy x = 3 hoặc x = -2

TL:
\(a,\sqrt{\left(\sqrt{3}-x\right)^2}=\sqrt{3}-x\)
BT thỏa mãn \(\forall x\)
a) \(\sqrt{\left(\sqrt{3}-x\right)^2}=\left|\sqrt{3}-x\right|\)
Vậy biểu thức có nghĩa với mọi x
b) \(\sqrt{\frac{-3}{2+x}}\)
Biểu thức có nghĩa\(\Leftrightarrow2+x< 0\Leftrightarrow x< -2\)
a) \(\sqrt{16x}=8\)
\(\Leftrightarrow\sqrt{16x}^2=8^2\)
\(\Leftrightarrow16x=64\Rightarrow x=\dfrac{64}{16}=4\)
b) \(\sqrt{4x}=\sqrt{5}\)
\(\Leftrightarrow\sqrt{4x}^2=\sqrt{5}^2\)
\(\Rightarrow4x=5\Rightarrow x=\dfrac{5}{4}\)
c) \(\sqrt{9\left(x-1\right)}=21\)
\(\Leftrightarrow\sqrt{9\left(x-1\right)}^2=21^2\)
\(\Leftrightarrow9\left(x-1\right)=441\)
\(\Leftrightarrow x-1=49\rightarrow x=50\)
d) \(\sqrt{4\left(1-x\right)^2}-6=0\)
\(\Leftrightarrow\sqrt{4\left(1-x\right)^2}^2=6^2\)
\(\Leftrightarrow4\left(1-x\right)^2=36\)
\(\Leftrightarrow\left(1-x\right)^2=9\)
\(\Rightarrow\left[{}\begin{matrix}x=-2\\x=4\end{matrix}\right.\)
a) Điều kiện x ≥ 0.
b) ĐS: x = .
.
c) ĐS: x = 50.
d) Điều kiện: Vì ≥ 0 với mọi giá trị của x nên
≥ 0 với mọi giá trị của x nên  có nghĩa với mọi giá trị của x.
có nghĩa với mọi giá trị của x.
Ta có 1 - x ≥ 0 khi x ≤ 1. Do đó:
khi x ≤ 1 thì │1 - x│ = 1 - x.
khi x > 1 thì │1 - x│ = x -1.
Để giải phương trình │1 - x│= 3, ta phải xét hai trường hợp:
- Khi x ≤ 1, ta có: 1 - x = 3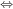 x = -2.
x = -2.
Vì -2 < 1 nên x = -2 là một nghiệm của phương trình.
- Khi x > 1, ta có: x - 1 = 3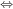 x = 4.
x = 4.
Vì 4 > 1 nên x = 4 là một nghiệm của phương trình.
Vậy phương trình có hai nghiệm là x = -2 và x = 4.