Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi các điểm thỏa mãn điều kiện có tọa độ là \(\left(a;0\right)\)
Khi đó hệ sau có nghiệm nguyên:\(\hept{\begin{cases}a-2y=3\\a-3y=2\\x-5y=-7\end{cases}\Rightarrow\frac{a-3}{2};\frac{a-2}{3};\frac{a+7}{5}}\) nguyên.
TH1: \(a\ge0.\)
\(\frac{a-3}{2}\in Z\) nên a lẻ; \(\frac{a+7}{5}\in Z\Rightarrow\) a chia 5 dư 3. Kết hợp hai điều kiện trên thì a có tận cùng là 3.
Khi đó a - 2 có tận cùng là 1. Vậy để \(\frac{a-2}{3}\in Z\) thì a - 2 = 34k \(\left(k\in N;k\ge1\right)\)
Vậy a = 2 +34k \(\left(k\in N;k\ge1\right)\)
TH2: a < 0
\(\frac{a-3}{2}\in Z\Rightarrow\)- a là số tự nhiên lẻ. \(\frac{a+7}{5}\in Z\Rightarrow\) -a chia 5 dư 2. Vậy -a có tận cùng là 7, vậy a có tận cùng là 7.
Vậy thì a - 2 có tận cùng là 9. Vậy a - 2 = -34k+2 \(\left(k\in N;k\ge0\right)\)
Hay a = 2 - 34k+2 \(\left(k\in N;k\ge0\right)\)
Tóm lại các điểm thỏa mãn điều kiện của đề bài sẽ có tọa độ là \(\left(2+3^{4k};0\right)\) với \(\left(k\in N;k\ge1\right)\) hoặc \(\left(2-3^{4k+2};0\right)\) với \(\left(k\in N;k\ge0\right)\)

Đồ thị hàm số y = ax + b cắt trục tung tại điểm có tung độ là b ; hoàng độ là -b/a
Vì A (4;3 ) thuộc đường thẳng thay x = 4 ; y = 3 vào hàm số ta đc :
3 = 4a + b => - b = 4a - 3 => \(-\frac{b}{a}=4-\frac{3}{a}\)
Theo bài ra ta có -b/a nguyên dương
=> 4 - 3/a nguyên dương => 3/a nguyên
Vì b > 0 => -b < 0 => -b/a > 0 khi a < 0
=> a thuộc ước âm của 3
=> a thuộc { -1 ; -3 }
(+) a = -1 => b = 7 => ta có đường thẳng y = -x + 7
(+) a= -3 ( tương tự )
cho hàm số: y=x2
a) vẽ đồ thị hàm số. ( tự vẽ được)
b) xác định các số a,b sao cho đường thẳng y=ax+b cắt trục tung tại điểm có tung độ bằng 2 và cắt đồ thị hàm số đã cho tại điểm có hoành độ bằng 1

- Từ hình vẽ ta có: yA = yB = 4 suy ra:.
+ Hoành độ của A: 4 = 2.xA => xA = 2 (*)
+ Hoành độ của B: 4 = xB => xB = 4
=> Tọa độ 2 điểm là: A(2, 4); B(4, 4)
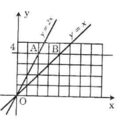
- Tìm độ dài các cạnh của ΔOAB
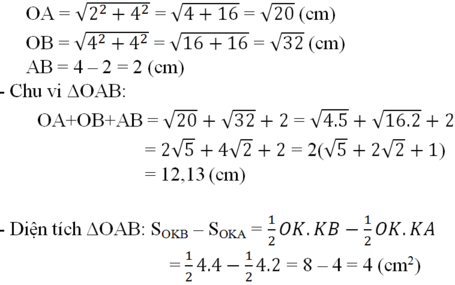
((*): muốn tìm tung độ hay hoành độ của một điểm khi đã biết trước hoành độ hay tung độ, ta thay chúng vào phương trình đồ thị hàm số để tìm đơn vị còn lại.)

b. Đồ thị đt đề cho là y=6
PTGD 2 đt đầu bài với đt câu b là: \(\left\{{}\begin{matrix}2x=6\\x-1=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\rightarrow A\left(3;6\right)\\x=7\rightarrow B\left(7;6\right)\end{matrix}\right.\)

Cô hướng dẫn nhé.
Giả sử điểm cầm tìm là M(a; 0). Như vậy, đường thẳng qua M, vuông góc với Ox là đường thẳng (d) : x = a.
Giao điểm của (d) với hai đường thẳng đã cho lần lượt là: \(A\left(a;\frac{2a-4}{3}\right)\) và \(B\left(a;\frac{3a-2}{5}\right)\)
Do a nguyên nên ta cầm tìm điều kiện để \(\frac{2a-4}{3}\) và \(\frac{3a-2}{5}\)nguyên.
Ta thấy \(\frac{2a-4}{3}=\frac{2\left(a-2\right)}{3}\)nên (a - 2) chia hết 3. Vậy thì a có dạng 3k + 2, (k nguyên dương).
\(\frac{3a-2}{5}=\frac{3a+3-5}{5}\) nên (3a + 3) chia hết 5 hay a + 1 chia hết 5. Vậy a có dạng 5t - 1, (t nguyên dương).
Kết hợp hai điều kiện: \(3k+2=5t-1\Leftrightarrow3\left(k+1\right)=5t\Leftrightarrow\frac{k+1}{5}=\frac{t}{3}.\)
a min thì k, t min nên ta tìm được k = 4, t = 3.
Vậy thi a = 14.
Bài này tương tự như bài cô đã chứng minh.
Gọi các điểm thỏa mãn yêu cầu có tọa độ \(\left(0;b\right)\)
Khi đó hệ sau có nghiệm nguyên \(\hept{\begin{cases}x+2b=6\\2x-3b=4\end{cases}\Rightarrow6-2b;\frac{4+3b}{2}\in Z.}\)
b nguyên nên 6 - 2b nguyên là hiển nhiên. Để \(\frac{4+3b}{2}\in Z\) thì b = 2k.
Vậy các điểm thỏa mãn sẽ có tọa độ là (0;2k) (\(k\in Z\) ).
cái này dễ mỗi tội tớ k biết làm