K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
1
CM
22 tháng 8 2018
*Ta có: 2x + y = 1 ⇔ y = -2x + 1
Cho x = 0 thì y = 1 ⇒ (0; 1)
Cho y = 0 thì x = 1/2 ⇒ (1/2 ; 0)
*Ta có: 4x – 2y = -10 ⇔ y = 2x + 5
Cho x = 0 thì y = 5 ⇒ (0; 5)
Cho y = 0 thì x = - 5/2 ⇒ (- 5/2 ; 0)
Hoành độ giao điểm của hai đường thẳng:
-2x + 1 = 2x + 5 ⇔ 4x = -4 ⇔ x = -1
Tung độ giao điểm của hai đường thẳng:
y = -2(-1) + 1 = 2 + 1 = 3
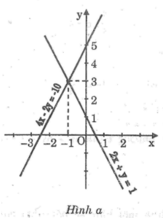
Vậy tọa độ giao điểm của hai đường thẳng là (-1; 3).
Đồ thị:
21 tháng 5 2022
b: Phương trình hoành độ giao điểm là:
\(\dfrac{-1}{2}x^2-4x+16=0\)
\(\Leftrightarrow x^2\cdot\dfrac{1}{2}+4x-16=0\)
\(\Leftrightarrow x^2+8x-32=0\)
\(\Leftrightarrow\left(x+4\right)^2=48\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\sqrt{3}-4\\x=-4\sqrt{3}-4\end{matrix}\right.\)
Khi \(x=4\sqrt{3}-4\) thì \(y=\dfrac{-1}{2}\cdot\left(4\sqrt{3}-4\right)^2=-32+16\sqrt{3}\)
Khi \(x=-4\sqrt{3}-4\) thì \(y=\dfrac{-1}{2}\left(-4\sqrt{3}-4\right)^2=-32-16\sqrt{3}\)
b: Để hai đường song song thì
\(\left\{{}\begin{matrix}m-1=-1\\m+3< >1\end{matrix}\right.\Leftrightarrow m=0\)
Mik chưa học đến lớp 9 nên chỉ tìm dc x, y thôi chứ tìm tọa độ mik chưa học.
\(\left[{}\begin{matrix}y=2x+4\\y=2x-3\end{matrix}\right.\) ⇔ \(\left[{}\begin{matrix}2x-y=-4\\2x-y=3\end{matrix}\right.\)
Dễ thấy Hệ Phương Trình không có nghiệm nào
=> HPT vô nghiệm
Lời giải:
Ta thấy hệ số góc của 2 đường thẳng bằng nhau (bằng $2$) nên 2 đường thẳng này song song
Do đó chúng không có giao điểm.