
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mặt phẳng (P) có vecto pháp tuyến \(\overrightarrow{p}=\left(1;1;1\right)\), ta có A' là hình chiếu của A trên (P) khi và chỉ khi \(\begin{cases}A'\in\left(P\right)\\AA'\perp\left(P\right)\end{cases}\)
Gọi \(A'\left(x;y;z\right)\) là hình chiếu của A trên (P). Khi đó, ta có hệ phương trình :
\(\begin{cases}x+y+z-3=0\\\frac{x-1}{1}=\frac{y-1}{1}=\frac{z-1}{1}\end{cases}\)
Giải hệ thu được :
\(z=-\frac{2}{3};x=\frac{4}{3};y=\frac{7}{3}\)
Vậy A' cần tìm là \(A'\left(\frac{4}{7};\frac{7}{3};-\frac{2}{3}\right)\)
Nếu A" là điểm đối xứng với A qua mặt phẳng (P) thì A' là trung điểm của AA". Từ đó suy ra \(A"\left(\frac{5}{3};\frac{8}{3};-\frac{1}{3}\right)\)

\(\overrightarrow{AB}=\left(-1;-2;1\right)\); \(\overrightarrow{n_{\alpha}}=\left(2;-1;2\right)\)\(\Rightarrow\overrightarrow{n_p}=\left[\overrightarrow{AB};\overrightarrow{n_{\alpha}}\right]=\left(-3;4;5\right)\)
Phương trình mặt phẳng (P) : \(-3x+4y+5z=0\)
\(R=d\left(A;\left(\alpha\right)\right)=\frac{\left|6-1+2+1\right|}{\sqrt{9}}=\frac{8}{3}\)
Phương trình mặt cầu (S) : \(\left(x-3\right)^2+\left(y-1\right)^2+\left(z-1\right)^2=\frac{64}{9}\)

Vecto pháp tuyến của mp α là n → =(2;-1;2), H là hình chiếu vuông góc của M trên mp α nên M H ⊥ m p α , đường thẳng MK có vecto pháp tuyến n → = ( 2 ; - 1 ; 2 )
Ta có pt tham số của đường thẳng MH là : x = 1 + 2 t y = - 1 - t z = 2 + 2 t
Thay x,y,z từ pt tham số của đường thẳng MH và pt mp α , ta có:
2(1+2t)-(-1-t)+2(2+2t)+11=0 <=> t=-2
Vậy H(-3;1;-2)

\(d\left(A,\left(\alpha\right)\right)=\frac{4}{3}\)
\(\left(\beta\right)\)//\(\left(\alpha\right)\) nên phương trình \(\left(\beta\right)\) có dạng : \(x+2y-2z+d=0,d\ne-1\)
\(d\left(A,\left(\alpha\right)\right)=d\left(A,\left(\beta\right)\right)\)\(\Leftrightarrow\frac{\left|5+d\right|}{3}=\frac{4}{3}\Leftrightarrow\begin{cases}d=-1\\d-9\end{cases}\)\(\Leftrightarrow d=-9\left(d=-1loai\right)\)\(\Rightarrow\left(\beta\right):x+2y-2z-9=0\)

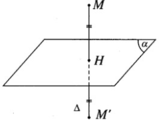
Phương trình tham số của đường thẳng ∆ đi qua điểm M(1; -1; 2) và vuông góc với mặt phẳng ( α ): 2x – y + 2z + 12 = 0 là:
Δ 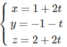
Xét điểm H(1 + 2t; -1 – t; 2 + 2t) ∈ ∆
Ta có H ∈ ( α ) ⇔ 2(1 + 2t) + (1 + t) + 2(2 + 2t) + 12 = 0 ⇔ t = −19/9
Vậy ta được ![]()





