Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét
\(y'=4x^3-4\left(m-1\right)x=0\Leftrightarrow\orbr{\begin{cases}x=0\\x^2=m-1\end{cases}}\)
TH1:
\(m-1\le0\) thì hàm số đồng biến trên R
TH2: \(m-1>0\Rightarrow\orbr{\begin{cases}x=\sqrt{m-1}\\x=-\sqrt{m-1}\end{cases}}\)
Khi đó khoảng đồng biến của hàm số là \(\left(-\infty,-\sqrt{m-1}\right)\text{ và }\left(0,\sqrt{m-1}\right)\)
Muốn hàm số đồng biến trên (1,3) thì \(\left(1,3\right)\subset\left(0,\sqrt{m-1}\right)\Leftrightarrow3\le\sqrt{m-1}\Leftrightarrow m\ge10\)
Vậy \(\orbr{\begin{cases}m\le1\\m\ge10\end{cases}}\)

Ta có : \(y'=4x^3-4\left(m-1\right)x\)
\(y'=0\Leftrightarrow4x^3-4\left(m-1\right)x=0\Leftrightarrow x\left[x^2-\left(m-1\right)\right]=0\)
Trường hợp 1 : nếu \(m-1\le0\Leftrightarrow m\le1\), hàm số đồng biến trên khoảng \(\left(0;+\infty\right)\), vậy \(m\le1\) thỏa mãn yêu cầu bài toán
Trường hợp 2 : nếu \(m-1>0\Leftrightarrow m>1\), hàm số đồng biến trên khoảng \(\left(-\sqrt{m-1};0\right)\) và \(\left(\sqrt{m-1};+\infty\right)\)
Để hàm số đồng biến trên khoảng (1;3) thì \(\left(\sqrt{m-1}\le1\Leftrightarrow m\le2\right)\)
Vậy hàm số đồng biến trên khoảng (1;3) \(\Leftrightarrow m\in\left(-\infty;2\right)\)

1.
\(y'=m-3cos3x\)
Hàm đồng biến trên R khi và chỉ khi \(m-3cos3x\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge3cos3x\) ; \(\forall x\)
\(\Leftrightarrow m\ge\max\limits_{x\in R}\left(3cos3x\right)\)
\(\Leftrightarrow m\ge3\)
2.
\(y'=1-m.sinx\)
Hàm đồng biến trên R khi và chỉ khi:
\(1-m.sinx\ge0\) ; \(\forall x\)
\(\Leftrightarrow1\ge m.sinx\) ; \(\forall x\)
- Với \(m=0\) thỏa mãn
- Với \(m< 0\Rightarrow\dfrac{1}{m}\le sinx\Leftrightarrow\dfrac{1}{m}\le\min\limits_R\left(sinx\right)=-1\)
\(\Rightarrow m\ge-1\)
- Với \(m>0\Rightarrow\dfrac{1}{m}\ge sinx\Leftrightarrow\dfrac{1}{m}\ge\max\limits_R\left(sinx\right)=1\)
\(\Rightarrow m\le1\)
Kết hợp lại ta được: \(-1\le m\le1\)

Đề yêu cầu tìm m sao cho hàm số đồng biến trên từng khoảng xác định K \(\left(-\infty,m\right),\left(m,+\infty\right)\)
\(y'=\dfrac{x^2-2mx+m^2-m+1}{\left(x-m\right)^2}\)
y đồng biến trên K \(\Leftrightarrow x^2-2mx+m^2-m+1\ge0,\forall x\in K\)
\(f\left(x\right)=x^2-2mx+m^2-m+1\ge0,\forall x\in K\) (1)
Nhận xét: f(x) là một parabol hướng lên và min tại \(x=m\)
(1) \(\Leftrightarrow\) \(f\left(m\right)\ge0\) \(\Leftrightarrow1\ge m\)
Vậy...
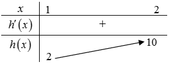
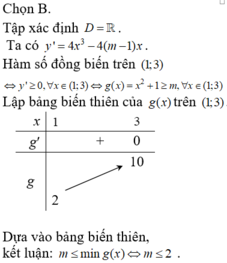
y'= \(4x^3-4\left(m-1\right)x\)
Để hàm số đồng biến trên khoảng (1;3) thì \(y'\left(x\right)\ge0,\forall x\in\left(1;3\right)\)
\(\Leftrightarrow x^2-\left(m-1\right)\ge0,\forall x\in\left(1;3\right)\)
\(\Leftrightarrow m-1\le x^2,\forall x\in\left(1;3\right)\)
\(\Rightarrow m-1\le1\Leftrightarrow m\le2\)
Vậy \(m\in\) (−\(\infty\);2]