Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trường hợp 1: \(m\ne\pm2\)
Để phương trình có đúng hai nghiệm phân biệt thì phương trình này sẽ có hai nghiệm trái dấu
=>\(m^2-4< 0\)
hay -2<m<2
Trường hợp 2: m=2
Pt sẽ là 1=0(vô lý)
Trường hợp 3: m=-2
=>-4x2+1=0(nhận)
Vậy: -2<=m<2

Phương trình đã cho nghiệm đúng với ∀ x ∈ R hay phương trình có vô số nghiệm khi m 2 − 1 = 0 m − 1 = 0 ⇔ m = 1
Đáp án cần chọn là: A

\(x-4\sqrt{x+3}+m=0\)
\(\Leftrightarrow x+3-4\sqrt{x+3}-3+m=0\left(1\right)\)
\(đăt:\sqrt{x+3}=t\left(t\ge0\right)\)
\(\left(1\right)\Leftrightarrow t^2-4t-3+m=0\Leftrightarrow f\left(t\right)=t^2-4t-3=-m\left(2\right)\)
\(\left(1\right)-có-2ngo-phân-biệt\Leftrightarrow\left(2\right)có-2ngo-phân-biệt-thỏa:t\ge0\)
\(\Rightarrow f\left(0\right)=-3\)
\(\Rightarrow f\left(t\right)min=\dfrac{-\Delta}{4a}=-7\Leftrightarrow t=2\)
\(\Rightarrow-7< -m\le-3\Leftrightarrow3\le m< 7\)
\(t^2-4t-3+m=0\Leftrightarrow t^2-4t-3=-m\)
\(có-2nghiệm-pb-trên[0;\text{+∞})\)
\(xét-bảng-biến-thiên-củaf\left(t\right)=t^2-4t-3,trên[0;\text{+∞})\)
f(t) 0 2 +∞ -∞ -3 -7 -m -m t
dựa vào bảng biến thiên ta thấy số nghiệm của phương trình f(t)
là số giao điểm của đường thẳng y=-m
\(\Rightarrow-7< -m\le-3\Leftrightarrow3\le m< 7\)

Đặt \(-x^2+2x=t\Rightarrow0\le t\le1\)
\(\Rightarrow-t^2+t-3+m=0\)
\(\Leftrightarrow t^2-t+3=m\)
Xét hàm \(f\left(t\right)=t^2-t+3\) trên \(\left[0;1\right]\)
\(-\dfrac{b}{2a}=\dfrac{1}{2}\in\left[0;1\right]\)
\(f\left(0\right)=3\) ; \(f\left(1\right)=3\) ; \(f\left(\dfrac{1}{2}\right)=\dfrac{11}{4}\)
\(\Rightarrow\dfrac{11}{4}\le f\left(t\right)\le3\)
\(\Rightarrow\) Pt có nghiệm khi và chỉ khi \(\dfrac{11}{4}\le m\le3\)

Phương trình đã cho nghiệm đúng với hay phương trình có vô số nghiệm khi
m 2 − 3 m + 2 = 0 − ( m 2 + 4 m + 5 ) = 0 ⇔ m = 1 m = 2 m ∈ ∅ ⇔ m ∈ ∅
Đáp án cần chọn là: D

Phương trình có hai nghiệm phân biệt ⇔ ∆ > 0
⇔ m 2 - 8 m + 16 = 0 m - 4 2 > 0 ⇔ m ≠ 4 *
Theo định lí Viet, ta có:
x 1 . x 2 = m − 1 3 ; x 1 + x 2 = m + 2 3 x 1 = 2 x 2 ⇔ x 1 = 2 9 ( m + 2 ) , x 2 = 1 9 ( m + 2 ) x 1 . x 2 = m − 1 3
⇒ 2 81 ( m + 2 ) 2 = m − 1 3 ⇔ 2 m 2 − 19 m + 35 = 0 ⇔ m = 5 2 m = 7 (thỏa mãn (*))
Đáp án cần chọn là: A

Chọn A.
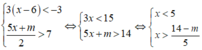
Hệ bất phương trình có nghiệm
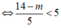 ⇔ 14 - m < 25 ⇔ -m < 11 ⇔ m > -11
⇔ 14 - m < 25 ⇔ -m < 11 ⇔ m > -11