Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=f\left(x\right)=3x^2+6x-3m\)
Để hàm số đồng biến trên \(\left(-\infty;0\right)\)
- TH1: \(\Delta'\le0\Rightarrow9+9m\le0\Rightarrow m\le-1\)
- TH2: \(\left\{{}\begin{matrix}\Delta'>0\\0\le x_1< x_2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\S>0\\P\ge0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>-1\\-2>0\\-m>0\end{matrix}\right.\) \(\Rightarrow\) ko có m thỏa mãn
Vậy \(m\le-1\)

Lời giải:
Ta có:
\(y=mx^3-2x^2+3mx+2016\)
\(\Rightarrow y'=3mx^2-4x+3m\)
Để hàm số luôn nghịch biến trên tập xác định \(y'\leq 0\) thì trước tiên cần có \(m\leq 0\) (1)
Với \(m\leq 0\), áp dụng định lý về dấu của tam thức bậc 2 ta có:
\(y'\leq 0\Leftrightarrow \Delta'=4-9m^2\leq 0\)
\(\Leftrightarrow \) \(\left[{}\begin{matrix}m\le\dfrac{-2}{3}\\m\ge\dfrac{2}{3}\end{matrix}\right.\) (2)
Từ \((1);(2)\Rightarrow m\leq \frac{-2}{3}\) thì hàm số luôn nghịch biến trên tập xác định.

Ta có y ' = - 3 x 2 + 6 x + 3 m . Hàm số nghịch biến trên khoảng (0; +∞) nếu y' ≤ 0 trên khoảng (o; +∞)
Cách 1: Dùng định lí dấu tam thức bậc hai.
Xét phương trình - 3 x 2 + 6 x + 3 m . Ta có Δ' = 9(1 + m)
TH1: Δ' ≤ 0 => m ≤ -1 khi đó, - 3 x 2 + 6 x + 3 m < 0 nên hàm số nghịch biến trên R .
TH2: Δ' > 0 => m > -1; y' = 0 có hai nghiệm phân biệt là x = 1 ±√(1+m) .
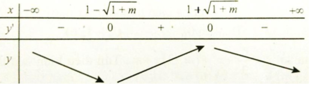
Hàm số nghịch biến trên (0; +∞) <=> 1 + √(1+m) ≤ 0, vô lí.
Từ TH1 và TH2, ta có m ≤ -1
Cách 2: Dùng phương pháp biến thiên hàm số.
Ta có y ' = - 3 x 2 + 6 x + 3 m ≤ 0 , ∀x > 0 <=> 3 m ≤ 3 x 2 - 6 x , ∀x > 0
Từ đó suy ra 3 m ≤ m i n ( 3 x 2 - 6 x ) với x > 0
Mà 3 x 2 - 6 x = 3 ( x 2 - 2 x + 1 ) - 3 = 3 ( x - 1 ) 2 - 3 ≥ - 3 ∀ x
Suy ra: m i n ( 3 x 2 – 6 x ) = - 3 khi x= 1
Do đó 3m ≤ -3 hay m ≤ -1.
Chọn đáp án C.

1.
\(y'=m-3cos3x\)
Hàm đồng biến trên R khi và chỉ khi \(m-3cos3x\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge3cos3x\) ; \(\forall x\)
\(\Leftrightarrow m\ge\max\limits_{x\in R}\left(3cos3x\right)\)
\(\Leftrightarrow m\ge3\)
2.
\(y'=1-m.sinx\)
Hàm đồng biến trên R khi và chỉ khi:
\(1-m.sinx\ge0\) ; \(\forall x\)
\(\Leftrightarrow1\ge m.sinx\) ; \(\forall x\)
- Với \(m=0\) thỏa mãn
- Với \(m< 0\Rightarrow\dfrac{1}{m}\le sinx\Leftrightarrow\dfrac{1}{m}\le\min\limits_R\left(sinx\right)=-1\)
\(\Rightarrow m\ge-1\)
- Với \(m>0\Rightarrow\dfrac{1}{m}\ge sinx\Leftrightarrow\dfrac{1}{m}\ge\max\limits_R\left(sinx\right)=1\)
\(\Rightarrow m\le1\)
Kết hợp lại ta được: \(-1\le m\le1\)

Để hàm số có 3 cực trị \(\Leftrightarrow m-2< 0\Rightarrow m< 2\)
\(y'=4x^3+4\left(m-2\right)x=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\sqrt{2-m}\\x=-\sqrt{2-m}\end{matrix}\right.\)
Gọi 3 cực trị lần lượt là A; B; C
\(\Rightarrow A\left(0;m^2-5m+6\right)\) ; \(B\left(-\sqrt{2-m};2-m\right)\) ; \(C\left(\sqrt{2-m};2-m\right)\)
Gọi I là trung điểm BC \(\Rightarrow I\left(0;2-m\right)\) ; \(BC=2\sqrt{2-m}\) ; \(AI=m^2-4m+4\)
Tam giác ABC đều khi và chỉ khi:
\(AI=\frac{\sqrt{3}}{2}BC\Leftrightarrow\left(2-m\right)^2=\sqrt{3\left(2-m\right)}\)
\(\Leftrightarrow\left(2-m\right)^3=3\Leftrightarrow m=2-\sqrt[3]{3}\)
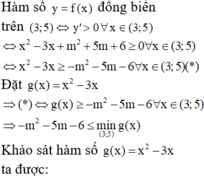
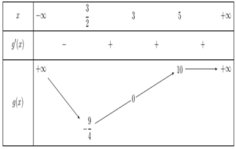


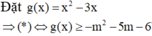
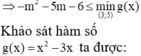

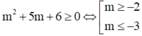
\(y'=3x^2-6mx\)
\(y'=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2m\end{matrix}\right.\)
Để hàm số đồng biến trên \(\left(4;+\infty\right)\) \(\Leftrightarrow2m\le4\Rightarrow m\le2\)