
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: (x3 +
)8=Ck8 x3(8 – k) ()k =Ck8 x24 – 4k
Trong tổng này, số hạng Ck8 x24 – 4k không chứa x khi và chỉ khi


bài này dễ thôi bạn
thay x= x+ k6pi vào hàm số y=f(x)= sin\(\frac{x}{3}\) ta dc
sin\(\frac{x+k6pi}{3}\) =sin\(\frac{x}{3}+k2pi\) ( vì k2pi "số chẵn lần của π" nên có thể bỏ được)
suy ra sin\(\frac{x}{3}\) =sin\(\frac{x}{3}\) =f(x) ( dpcm)

\(e.y=2sin^2x-cos2x=1-cos2x-cos2x=1-2cos2x\)
Vì \(-1\le cos2x\le1\Leftrightarrow-2\le-2cos2x\le2\Leftrightarrow-1\le1-2cos2x\le3\)
Vậy \(y_{max}=3khicos2x=-1\Leftrightarrow x=\frac{\pi}{2}+k\pi\) \(y_{min}=-1khicos2x=-1\Leftrightarrow cos2x=1\Leftrightarrow x=k\pi\)


ĐKXĐ: \(-2\le x\le3\)
Đặt \(\sqrt{x+2}+2\sqrt{3-x}=a\Rightarrow4\sqrt{6+x-x^2}-3x=a^2-14\)
Mặt khác \(a^2=\left(\sqrt{x+2}+2\sqrt{3-x}\right)^2\le5\left(x+2+3-x\right)=25\)
\(\Rightarrow a\le5\)
Và \(\sqrt{x+2}+\sqrt{3-x}+\sqrt{3-x}\ge\sqrt{5}+\sqrt{3-x}\ge\sqrt{5}\) \(\Rightarrow a\ge\sqrt{5}\)
\(\Rightarrow\sqrt{5}\le a\le5\)
Phương trình trở thành:
\(a^2-14=ma\Leftrightarrow\frac{a^2-14}{a}=m\) với \(a\in\left[\sqrt{5};5\right]\)
\(f\left(a\right)=\frac{a^2-14}{a}\Rightarrow f'\left(a\right)=\frac{2a^2-a^2+14}{a^2}=\frac{a^2+14}{a^2}>0\)
\(\Rightarrow f\left(a\right)\) đồng biến \(\Rightarrow f\left(\sqrt{5}\right)\le f\left(a\right)\le5\)
\(\Rightarrow-\frac{9\sqrt{5}}{5}\le f\left(a\right)\le\frac{11}{5}\Rightarrow-\frac{9\sqrt{5}}{5}\le m\le\frac{11}{5}\)
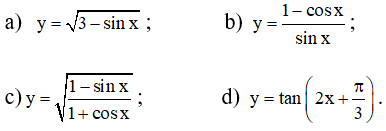
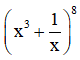

 ghgfh
ghgfh

 em đang bí quá, giúp em với ạ, đề thi thử toán 11
em đang bí quá, giúp em với ạ, đề thi thử toán 11




a) Vì -1 ≤ sinx ≤ 1 nên 3 - sinx > 0 với mọi x nên tập xác định của hàm số là D = R.
b) y = (1 - cosx)/sinx xác định khi và chỉ khi sinx ≠ 0
⇔ x ≠ kπ, k ∈ Z.
Vậy tập xác định D = R\{kπ|k ∈ Z}
c) Vì 1 - sinx ≥ 0 và 1 + cosx ≥ 0 nên hàm số xác định khi và chỉ khi
cosx ≠ -1 ⇔ x ≠ π + k2π, k ∈ Z.
Vậy tập xác định D = R\{π + k2π|k ∈ Z}
a, \(D=R\)