VV
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 11 2018
Nhầm xíu, quên không khai căn, thế này mới đúng :D
\(y=\dfrac{\sqrt{26}}{5}\left(\dfrac{5\sqrt{26}}{26}sinx+\dfrac{\sqrt{26}}{26}cosx\right)=\dfrac{\sqrt{26}}{5}sin\left(x+\alpha\right)\)
Với \(\alpha=arccos\dfrac{5\sqrt{26}}{26}\)
Do \(-1\le sin\left(x+\alpha\right)\le1\Rightarrow\dfrac{-\sqrt{26}}{5}\le y\le\dfrac{\sqrt{26}}{5}\)
\(\Rightarrow\left\{{}\begin{matrix}y_{min}=\dfrac{-\sqrt{26}}{5}\\y_{max}=\dfrac{\sqrt{26}}{5}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 11 2018
\(y=\dfrac{26}{25}\left(\dfrac{25}{26}sinx+\dfrac{5}{26}.cosx\right)=\dfrac{26}{25}sin\left(x+\alpha\right)\) với \(\alpha=arccos\dfrac{25}{26}\)
Do \(-1\le sin\left(x+\alpha\right)\le1\) \(\Rightarrow\dfrac{-26}{25}\le y\le\dfrac{26}{25}\)
\(\Rightarrow y_{min}=-\dfrac{26}{25}\) ; \(y_{max}=\dfrac{26}{25}\)
MM
1
27 tháng 5 2021
a) Hàm số xđ <=> \(1+cos2x>0\) \(\Leftrightarrow cos2x\ne-1\) \(\Leftrightarrow\)\(2cos^2x-1\ne-1\)
\(\Leftrightarrow cosx\ne0\) \(\Leftrightarrow x\ne\dfrac{\pi}{2}+k\pi\left(k\in Z\right)\)
b)Hàm số xđ <=> \(1-sinx>0\) \(\Leftrightarrow sinx\ne1\) \(\Leftrightarrow x\ne\dfrac{\pi}{2}+k2\pi\left(k\in Z\right)\)
c) Hàm số xđ <=> \(sinx+cos5x\ne0\)
\(\Leftrightarrow sinx\ne-cos5x\)
\(\Leftrightarrow cos\left(\dfrac{\pi}{2}-x\right)\ne cos\left(\pi-5x\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{\pi}{2}-x\ne\pi-5x+k2\pi\\\dfrac{\pi}{2}-x\ne-\pi+5x+k2\pi\end{matrix}\right.\) (\(k\in Z\))
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{8}+\dfrac{k\pi}{2}\\x\ne\dfrac{\pi}{4}-\dfrac{k\pi}{3}\end{matrix}\right.\)(\(k\in Z\))
d) Hàm số xđ <=> \(sinx-\sqrt{3}cosx\ne0\)
\(\Leftrightarrow2.sin\left(x-\dfrac{\pi}{3}\right)\ne0\) \(\Leftrightarrow x\ne\dfrac{\pi}{3}+k\pi\left(k\in Z\right)\)
e) Hàm số xđ <=> \(\left(sinx+1\right).cosx\ne0\)
\(\Leftrightarrow\left\{{}\begin{matrix}sinx\ne-1\\cosx\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne-\dfrac{\pi}{2}+k2\pi\\x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\) (\(k\in Z\)) \(\Rightarrow x\ne\dfrac{\pi}{2}+k\pi\) (Hai họ nghiệm trùng nhau nên e tổng hợp lại, e nghĩ thế)
f) Hàm số xđ <=> \(\left\{{}\begin{matrix}\left(1-tanx\right)\left(1-cotx\right)\ne0\\sinx\ne0\\cosx\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}tanx\ne1\\cotx\ne1\\sinx.cosx\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sinx\ne cosx\\\dfrac{1}{2}.sin2x\ne0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}sinx\ne sin\left(\dfrac{\pi}{2}-x\right)\\2x\ne k\pi\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{2}-x+k2\pi\\x\ne\dfrac{\pi}{2}+x+k2\pi\\x\ne\dfrac{k\pi}{2}\end{matrix}\right.\)(\(k\in Z\))
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{4}+k\pi\\0\ne\dfrac{\pi}{2}+k2\pi\\x\ne\dfrac{k\pi}{2}\end{matrix}\right.\)(\(k\in Z\)) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{4}+k\pi\\x\ne\dfrac{k\pi}{2}\end{matrix}\right.\)(\(k\in Z\))
PN
11 tháng 8 2020
những câu hỏi không liên quan đến THCS thì bạn vào h để có thể được giải đáp tốt hơn
18 tháng 7 2020
a) ĐK: \(\cos x\ne0\)( vì tan x = sinx/cosx nên cos x khác 0)
<=> \(x\ne\frac{\pi}{2}+k\pi\); k thuộc Z
TXĐ: \(ℝ\backslash\left\{\frac{\pi}{2}+k\pi\right\}\); k thuộc Z
b) ĐK: \(1+\cos2x\ne0\Leftrightarrow\cos2x\ne-1\Leftrightarrow2x\ne\pi+k2\pi\Leftrightarrow x\ne\frac{\pi}{2}+k\pi\); k thuộc Z
=> TXĐ: \(ℝ\backslash\left\{\frac{\pi}{2}+k\pi\right\}\); k thuộc Z
c) ĐK: \(\hept{\begin{cases}\cot x-\sqrt{3}\ne0\\\sin x\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ne\frac{\pi}{6}+k\pi\text{}\text{}\\x\ne l\pi\end{cases}}\); k,l thuộc Z
=>TXĐ: ....
d) ĐK: \(1-2\sin^2x\ne0\Leftrightarrow\cos2x\ne0\Leftrightarrow2x\ne\frac{\pi}{2}+k\pi\Leftrightarrow x\ne\frac{\pi}{4}+\frac{k\pi}{2}\)
=> TXĐ:...
AN
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
Hàm là vậy phải không nhỉ? \(y=\dfrac{sin^2x-3sinx}{\left(tanx-1\right)\left(cotx+1\right)}\)
ĐKXĐ: \(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\\tanx-1\ne0\\cotx+1\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sin2x\ne0\\tanx\ne1\\cotx\ne-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{k\pi}{2}\\x\ne\dfrac{\pi}{4}+k\pi\\x\ne-\dfrac{\pi}{4}+k\pi\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{k\pi}{2}\\x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\end{matrix}\right.\)
\(\Leftrightarrow x\ne\dfrac{k\pi}{4}\)
G
1
HP
9 tháng 8 2021
\(y=\dfrac{cos3x}{1-sinx}+tanx=\dfrac{cos3x}{1-sinx}+\dfrac{sinx}{cosx}\)
Hàm số xác định khi \(\left\{{}\begin{matrix}1-sinx\ne0\\cosx\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}sinx\ne1\\cosx\ne0\end{matrix}\right.\Leftrightarrow x\ne\dfrac{\pi}{2}+k\pi\)
27 tháng 6 2021
\(1.\hept{\begin{cases}2-2\cos x\ge0\\\sqrt{2-2\cos x}-2\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}\cos x\le1\left(đ\right)\\\cos x\ne-1\end{cases}}\Leftrightarrow x\ne\pi+k2\pi\left(k\in Z\right)\)
\(2.\hept{\begin{cases}\sin3x\ne0\\1+\sin3x\ge0\\1-\sqrt{1+\sin3x}\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}3x\ne k\pi\\\sin3x\ge-1\left(đ\right)\\\sin3x\ne0\end{cases}}\Leftrightarrow x\ne\frac{k\pi}{3}\left(k\in Z\right)\)
\(3.\hept{\begin{cases}\sin2x\ne0\\\sin x\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}2x\ne k\pi\\x\ne k\pi\end{cases}}\Leftrightarrow x\ne\frac{k\pi}{2}\left(k\in Z\right)\)
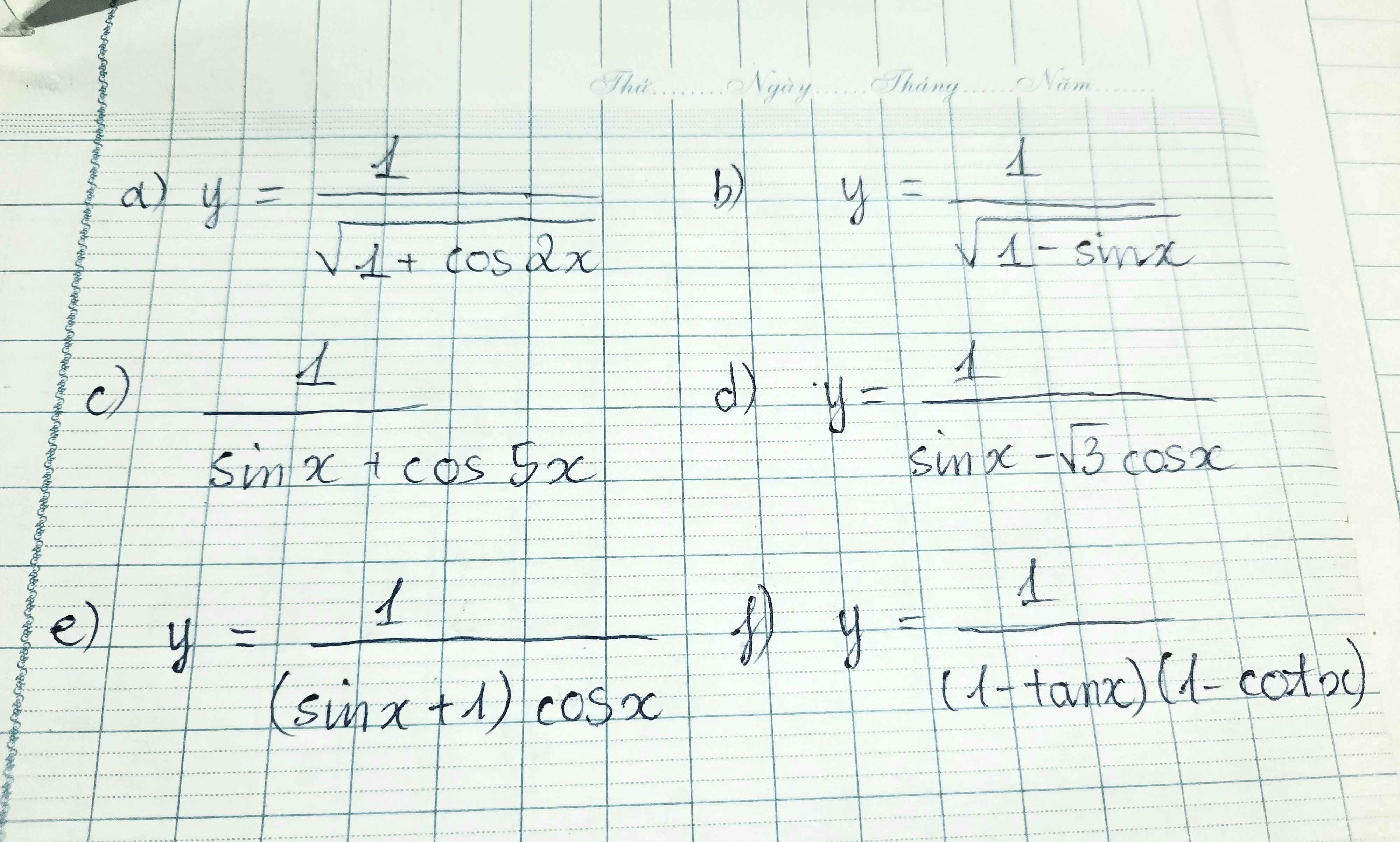
ĐKXĐ: \(sinx\ne1\Rightarrow x\ne\frac{\pi}{2}+k2\pi\)
(Không cần tìm điều kiện cho căn thức vì biểu thức luôn không âm)