Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
![]()
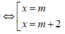
Do đó ta có bảng biến thiên sau:
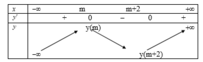
Để hàm số nghịch biến trên khoảng (-1;1) thì
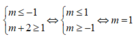

\(y'=f\left(x\right)=3x^2+6x-3m\)
Để hàm số đồng biến trên \(\left(-\infty;0\right)\)
- TH1: \(\Delta'\le0\Rightarrow9+9m\le0\Rightarrow m\le-1\)
- TH2: \(\left\{{}\begin{matrix}\Delta'>0\\0\le x_1< x_2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\S>0\\P\ge0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>-1\\-2>0\\-m>0\end{matrix}\right.\) \(\Rightarrow\) ko có m thỏa mãn
Vậy \(m\le-1\)

\(y'=-3x^2+6x+m\)
Để hàm số nghịch biến trên \(\left(0;+\infty\right)\Rightarrow y'\le0\) \(\forall x>0\)
\(\Rightarrow-3x^2+6x+m\le0\Leftrightarrow3x^2-6x\ge m\)
Đặt \(f\left(x\right)=3x^2-6x\Rightarrow m\le\min\limits_{\left(0;+\infty\right)}f\left(x\right)=f\left(1\right)=-3\)
\(\Rightarrow m\le-3\)


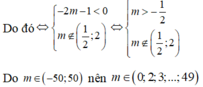

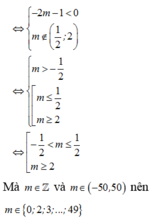

Chọn B