
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
Ký hiệu B là biến cố lấy được số tự nhiên A thỏa mãn yêu cầu bài toán.
Ta có 3N = A <=> N = log3A
Để N là số tự nhiên thì A = 3m (m ∈ N)
Những số A dạng có 4 chữ số gồm 37 = 2187 và 38 = 6561
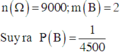

Chọn C
Vế trái của đẳng thức bằng (3-1)n =2n, Do đó 2n = 2048=211, suy ra n=11

Chứng minh: 3n > 3n + 1 (1)
+ Với n = 2 thì (1) ⇔ 9 > 7 (luôn đúng).
+ Giả sử (1) đúng với n = k ≥ 2, tức là 3k > 3k + 1.
Ta chứng minh đúng với n= k+1 tức là chứng minh: 3k+ 1 > 3(k+1) + 1
Thật vậy, ta có:
3k + 1 = 3.3k > 3.(3k + 1) (Vì 3k > 3k + 1 theo giả sử)
= 9k + 3
= 3k + 3 + 6k
= 3.(k + 1) + 6k
> 3(k + 1) + 1.( vì k ≥ 2 nên 6k ≥ 12> 1)
⇒ (1) đúng với n = k + 1.
Vậy 3n > 3n + 1 đúng với mọi n ≥ 2.

\(u_n=3n+1\left(n\in N^{\cdot}\right)\) là công thức tổng quát của dãy \(\left(u_n\right)\) mà mỗi số hạng của nó là số tự nhiên chia hết cho 3 dư 1 nên chọn câu A

Biết câu 2. Muốn chia hết 1995 thì số tận cùng phảl là 0 hoặc 5. Bạn thay n bằng các số từ 0 đến 9. Ko số nào đáp ứng điều kiện cả. Nên ko tồn tại.

Chọn A
Số phần tử của không gian mẫu: ![]() .
.
Gọi A là biến cố “Số lấy được là bình phương của một số tự nhiên”.
Bình phương của một số tự nhiên có dạng: ![]()
Ta có ![]() .
.
Vậy 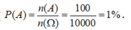 .
.
 Xài cái này gõ bài đi bạn, thề như này hiểu chết liền á :(
Xài cái này gõ bài đi bạn, thề như này hiểu chết liền á :(
\(\text{Ta có:} \ 3n \ \vdots \ 3 \Rightarrow 3n+2 \ \text{chia 3 dư 2} \\ \text{Mà một số chính phương khi chia 3 chỉ dư 0 hoặc 1} \\ \Rightarrow \text{Không tồn tại số tự nhiên} \ n \ \text{thỏa mãn}\)