Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(=\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+\dfrac{2}{7.9}+\dfrac{2}{9.11}+\dfrac{2}{11.13}\)
\(=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{13}\)
\(=1-\dfrac{1}{13}=\dfrac{12}{13}\)

a) A = {\(\dfrac{1}{n\left(n+1\right)}\)| \(n\in\mathbb{N},1\le n\le5\)}
b) B = {\(\dfrac{1}{n^2-1}\)|\(n\in\mathbb{N},2\le n\le6\)\(\)}

B={x\(\in\)N|x=3k; 1<=k<=4}
C={x\(\in\)N|x=4*a2; 1<=a<=5}
D={x\(\in\)N|x=9*a2;1<=a<=4}
E={x\(\in\)N|x=4k; 0<=x<=4}
G={x\(\in\)N|x=(-3)^k; 1<=k<=4}

a) \(A=\left\{x\in N|x=3k+1;0\le k\le3;k\in z\right\}\)
b) \(B=\left\{x\in Q^+|x=\dfrac{k}{k^2-1};2\le k\le6;k\in N\right\}\)

a: \(=\dfrac{54-34}{189-119}=\dfrac{20}{70}=\dfrac{2}{7}\)
b: \(=\dfrac{6+6\cdot4+6\cdot49}{15+15\cdot4+15\cdot49}=\dfrac{6}{15}=\dfrac{2}{5}\)
c: \(=\dfrac{13\left(3-18\right)}{40\left(15-2\right)}=\dfrac{-15}{40}=-\dfrac{3}{8}\)

\(A=\left\{x\in Q|x=\frac{k}{k^2-1},2\le k\le6,k\in Z\right\}\)
\(B=\left\{x\in Z|x=k^2-1,1\le k\le6,k\in Z\right\}\)

ĐKXĐ:
a/ \(\left\{{}\begin{matrix}x^2+2x-8\ne0\\x^2+2x-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ne-4\\x\ne2\\x\ne1\\x\ne-3\end{matrix}\right.\)
b/ \(x^2-2x+3\ge0\Rightarrow x\in R\)

\(\Leftrightarrow\dfrac{x+1}{\left(x+1\right)^2-1}+\dfrac{x+6}{\left(x+6\right)^2-1}=\dfrac{x+2}{\left(x+2\right)^2-1}=\dfrac{x+5}{\left(x+5\right)^2-1}\)
\(\Leftrightarrow\left(x+1\right)\left(x+6\right)^2-x-1+\left(x+6\right)\left(x+1\right)^2-x-6=\left(x+2\right)\left(x+5\right)^2-x-2+\left(x+5\right)\left(x+2\right)^2-x-5\)
=>(x+1)(x+6)^2+(x+6)(x+1)^2=(x+2)(x+5)^2+(x+2)^2(x+5)
=>(x+1)(x+6)(x+6+x+1)=(x+2)(x+5)(x+5+x+2)
=>(2x+7)[x^2+7x+6-x^2-7x-10]=0
=>(2x+7)=0
=>x=-7/2
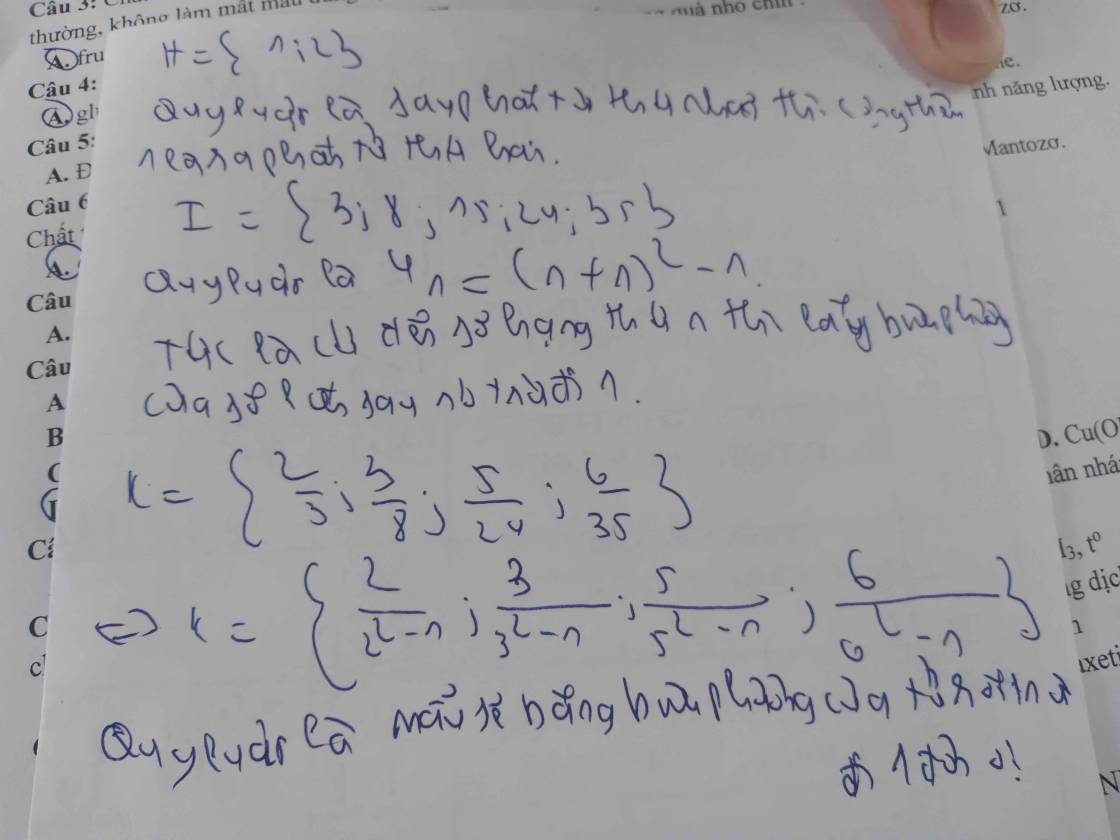
a) Gọi số hạng thứ 100 của dãy là n (n \(\in\) N)
TA có: 3=3
8= 3+5
15 = 3+5+7
24 = 3+5+7+9
35 = 3+5+7+9+11
n=3 + 5 + 7+ 9+11+...+n1
n1 = (100-1) . 2 + 3 = 201
=> n =(201+3) . 100 : 2 = 10200
Vậy số hạng thứ 100 của dãy n là 10200
b tương tự