K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
4 tháng 11 2017
Chọn A
Tìm tọa độ giao điểm M bằng cách giải hệ. Mặt phẳng (P) cần tìm qua điểm M và nhận vecto chỉ phương của d làm vecto pháp tuyến.

CM
6 tháng 3 2019
Đáp án C
Do a là giao điểm của ( α ) và ( β ) nên a và d cắt nhau.

CM
27 tháng 1 2017
Chọn đáp án A.
Cách 1: Đường thẳng d có một vectơ chỉ phương là

Cách 2: Vì mặt phẳng α chứa đường thẳng d nên α có phương trình


CM
28 tháng 6 2017
Chọn D
Từ phương trình hai mặt phẳng (P1), (P2) cho z = 1 ta tìm được điểm A(2;2;1) thuộc mặt phẳng (α) Tìm vecto chỉ phương của đường thẳng d. Vecto pháp tuyến của mặt phẳng cần tìm là tích có hướng của vecto pháp tuyến (P) và vecto chỉ phương của d



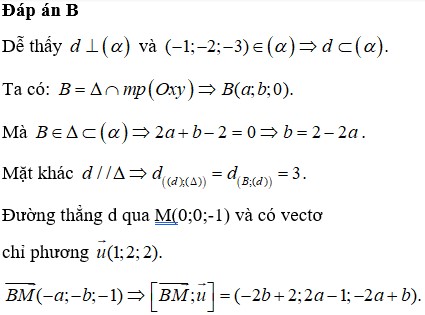
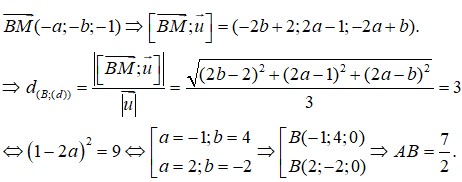



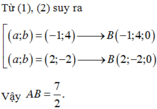
a) Thay các tọa độ x ; y ; z trong phương trình tham số của d vào phương trình (α) ta có:
3(12 + 4t) +5(9 + 3t) - (1 + t) = 0
⇔ 26t + 78 = 0 ⇔ t = -3.
Tức là d ∩ (α) = M(0 ; 0 ; -2).
Trong trường hợp này d cắt (α) tại điểm M.
b) Thay các tọa độ x ; y ; z trong phương trình tham số của d vào phương trình (α) ta có:
(1 + t) + 3.(2 - t) + (1 + 2t) + 1 = 0
⇔ 0.t + t = 9, phương trình vô nghiệm.
Chứng tỏ d và (α) không cắt nhau., ta có d // (α).
c) Thay các tọa độ x ; y ; z trong phương trình tham số của d vào phương trình (α) ta có:
(1 + 1) + (1+ 2t) + (2 - 3t) - 4 = 0
⇔ 0t + 0 = 0,phương trình này có vô số nghiệm, chứng tỏ d ⊂ (α) .