Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cả 2 phần cậu đều áp dụng tính chất dãy tỉ số bằng nhau đi
dễ mà

Bạn tham khảo ở đây: https://olm.vn/hoi-dap/detail/1284076363999.html
ΔABCΔABC có ˆA+ˆB+ˆC=180oA^+B^+C^=180o
Theo để bài ˆA3=ˆB4=ˆC5A^3=B^4=C^5
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
ˆA3=ˆB4=ˆC5=ˆA+ˆB+ˆC3+4+5=180o12=15oA^3=B^4=C^5=A^+B^+C^3+4+5=180o12=15o
hay: ˆA3=15o⇒ˆA=15o.3=45oA^3=15o⇒A^=15o.3=45o
ˆB4=15o⇒ˆB=15o.4=60oB^4=15o⇒B^=15o.4=60o
ˆC5=15o⇒ˆC=15o.5=75o

`a,` Gọi số đo `3` góc của Tam giác `ABC` lần lượt là `x,y,z (x,y,z \ne 0)`
Tỉ lệ thức biểu diễn mối quan hệ giữa số đo `3` góc trong Tam giác `ABC` là `x/2=y/3=z/4`
`b,` Tổng số đo `3` góc trong `1` tam giác là `180^0`
`-> x+y+z=180`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/2=y/3=z/4=(x+y+z)/(2+3+4)=180/9=20`
`-> x/2=y/3=z/4=20`
`->x=20*2=40, y=20*3=60, z=20*4=80`
Vậy, số đo của `3` góc trong Tam giác `ABC` lần lượt là `40^0, 60^0, 80^0.`
a:
Đặt \(a=\widehat{A};b=\widehat{B};c=\widehat{C}\)
a/2=b/3=c/4
b: a/2=b/3=c/4=(a+b+c)/(2+3+4)=180/9=20
=>a=40; b=60; c=80

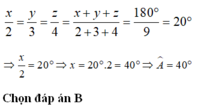
Gọi các góc của \(\Delta ABC\) là :a,b,c
a, Ta có : \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4};a+b+c=180^o\)
Áp dụng t/c dtsbn , ta có:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{180^o}{9}=20^o\)
\(\Rightarrow\left\{{}\begin{matrix}a=40^o\\b=60^o\\c=80^o\end{matrix}\right.\)
\(\Rightarrow\)Số đo các góc của \(\Delta ABC:....\)
b,Ta có : \(\dfrac{a}{1}=\dfrac{b}{2}=\dfrac{c}{3};a+b+c=180^o\)
Áp dụng t/c dtsbn , ta có :
\(\dfrac{a}{1}=\dfrac{b}{2}=\dfrac{c}{3}=\dfrac{a+b+c}{1+2+3}=\dfrac{180^o}{6}=30^o\)
\(\Rightarrow\left\{{}\begin{matrix}a=30^o\\b=60^o\\c=90^o\end{matrix}\right.\)
\(\Rightarrow\)Số đo các góc của \(\Delta ABC\):...
Gọi số đo ba góc của tg lần lượt là: \(a,b,c\left(a,b,c>0\right)\)
Áp dụng t/c dtsbn:
a. \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{180^0}{9}=20\)
\(\Rightarrow\left\{{}\begin{matrix}a=40^0\\b=60^0\\c=80^0\end{matrix}\right.\)
câu b lm tương tự nhé!