
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Gọi số đó là abc.
Ta có abc=37x+2=11y+5 với x,y thuộc N và x thuộc [3,26], y thuộc [9,90].
Từ pt 37x+2=11y+5 suy ra y=(37x-3)/11.
Thay các giá trị của x vào rồi đối chiếu đk suy ra có 2 giá trị tìm là x=9;20
suy ra abc=335 và 742
Cho 3a>2b>0 và 9a2+4b2=13ab.Tính giá trị biểu thức A=\(\frac{ab}{9a^2-4b^2}\)


(4x-9)(7x+4)=0
TH1: 4x-9 = 0
4x = 9
x = 9/4
TH2: 7x+4 = 0
7x = -4
x = -4/7

Biểu diễn y theo x :
\(\left(2x+3\right)y=5x+11\)
Dễ thấy :\(2x+3\) khác \(0\) (vì x là số nguyên) do đó:
\(y=\frac{5x+11}{2x+3}=2+\frac{x+5}{2x+3}\)
Để \(y\) \(\in\) \(Z\) thì \(x+5\) chia hết cho \(2x+3\)
\(\implies\) \(2.\left(x+5\right)\) chia hết cho \(2x+3\)
\(\implies\) \(2x+10\) chia hết cho \(2x+3\)
\(\implies\) \(2x+3+7\) chia hết cho \(2x+3\)
\(\implies\) \(7\) chia hết cho \(2x+3\)
\(\implies\) \(2x+3\) \(\in\) \(Ư\)(\(7\))={ \(1;-1;7;-7\) }
Ta có bảng sau:
| \(2x+3\) | \(1\) | \(-1\) | \(7\) | \(-7\) |
| \(x\) | \(-1\) | \(-2\) | \(2\) | \(-5\) |
| \(y\) | \(6\) | \(-1\) | \(3\) | \(2\) |
Vậy \(\left(x;y\right)\) \(\in\) {\(\left(-1;6\right),\left(-2;-1\right),\left(2;3\right),\left(-5;2\right)\) }

Biểu diễn y theo x :
\(\left(2x+3\right)y=5x+11\)
Dễ thấy :\(2x+3\) khác \(0\) (vì x là số nguyên) do đó:
\(y=\frac{5x+11}{2x+3}=2+\frac{x+5}{2x+3}\)
Để \(y\) \(\in\) \(Z\) thì \(x+5\) chia hết cho \(2x+3\)
\(\implies\) \(2.\left(x+5\right)\) chia hết cho \(2x+3\)
\(\implies\) \(2x+10\) chia hết cho \(2x+3\)
\(\implies\) \(2x+3+7\) chia hết cho \(2x+3\)
\(\implies\) \(7\) chia hết cho \(2x+3\)
\(\implies\) \(2x+3\) \(\in\) \(Ư\)(\(7\))={ \(1;-1;7;-7\) }
Ta có bảng sau:
| \(2x+3\) | \(1\) | \(-1\) | \(7\) | \(-7\) |
| \(x\) | \(-1\) | \(-2\) | \(2\) | \(-5\) |
| \(y\) | \(6\) | \(-1\) | \(3\) | \(2\) |
Vậy \(\left(x;y\right)\) \(\in\) {\(\left(-1;6\right),\left(-2;-1\right),\left(2;3\right),\left(-5;2\right)\) }

16: Tìm nghiệm nguyên của phương trình
x2 –xy + y2 = 3
Hướng dẫn:
Ta có x2 –xy + y2 = 3 ⇔ (x- )2 = 3 –
Ta thấy (x- )2 = 3 –
≥ 0
⇒ -2 ≤ y ≤ 2
⇒ y= ± 2; ±1; 0 thay vào phương trình tìm x
Ta được các nghiệm nguyên của phương trình là :
(x, y) = (-1,-2), (1, 2); (-2, -1); (2,1) ;(-1,1) ;(1, -1)
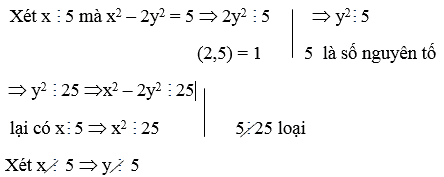
\(2xy-4x+y-9=0\)
\(\Leftrightarrow2x\left(y-2\right)+\left(y-2\right)-7=0\)
\(\Leftrightarrow\left(2x+1\right)\left(y-2\right)=7\)
\(\Rightarrow2x+1\) và \(y-2\) là ước của 7
đến đây dễ rồi tự làm nha
x=0 và y=9 ; x=3 và y=3
x=-1 và y=-5 ; x=-4 và y=1
đúng ko nhỉ