Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có :\(\left(\frac{3}{2}-\frac{5}{11}-\frac{3}{13}\right).\left(2x-2\right)=\left(-\frac{3}{4}+\frac{5}{22}+\frac{3}{26}\right)\)
=> \(\left(\frac{3}{2}-\frac{5}{11}-\frac{3}{13}\right).\left(2x-2\right)=-\frac{1}{2}\left(\frac{3}{2}-\frac{5}{11}-\frac{3}{13}\right)\)
=> \(2x-2=-\frac{1}{2}\)
=> \(2x=\frac{3}{2}\)
=> \(x=\frac{3}{4}\)

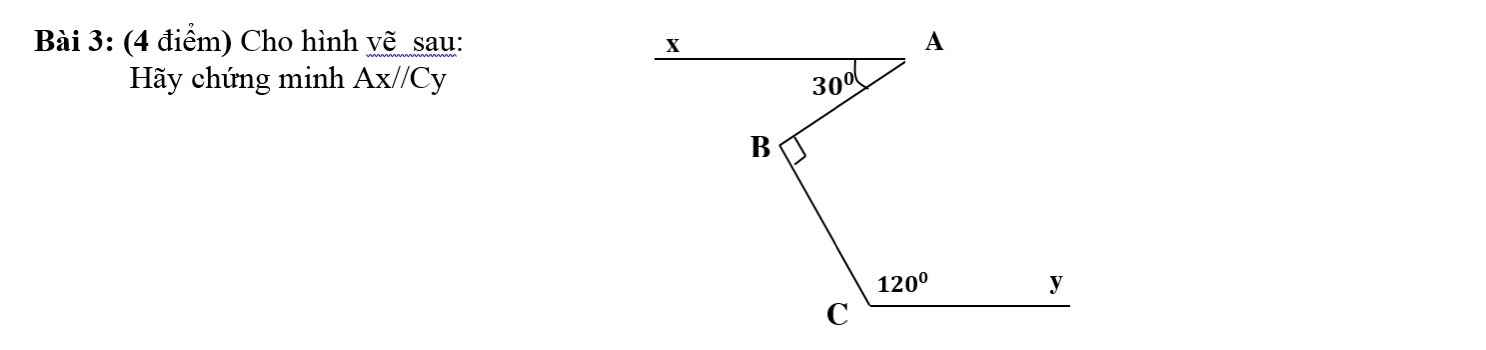
Kẻ Bz//Ax
Ta có: Ax//Bz
\(\Rightarrow\widehat{BAx}=\widehat{ABz}=30^0\)(so le trong)
\(\Rightarrow\widehat{zBC}=\widehat{ABC}-\widehat{BAx}=90^0-30^0=60^0\)
Ta có: \(\widehat{zBC}+\widehat{BCy}=60^0+120^0=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> Bz//Cy
Mà Bz//Ax
=> Ax//Cy

a)f(x)+g(x)=10xmũ2-8x+ 14/3
b)f(x)-g(x)=10x mũ 2 +4x+16/3
nghiệm chưa tính ddcj nha
a;\(f\left(x\right)+g\left(x\right)=\left(5x^2-2x+5\right)+\left(5x^2-6x-\frac{1}{3}\right)=25x^2-8x+\frac{1}{4}\)
b'\(f\left(x\right)-g\left(x\right)=\left(5x^2-2x+5\right)-\left(5x^2-6x-\frac{1}{3}\right)=4x+\frac{16}{3}\)
c;\(f\left(x\right)-g\left(x\right)=0\Leftrightarrow4x+\frac{16}{3}=0\)
\(\Leftrightarrow4x=-\frac{16}{3}\)
\(\Leftrightarrow x=-\frac{4}{3}\)
Vậy nghiệm của đa thức f(x)-g(x) là : x=-4/3

Ta có: x2 + 2x + 3
= x2 + x + x + 1 + 2
= (x2 + x) + (x + 1) + 2
= x(x + 1) + (x + 1) + 2
= (x + 1)(x + 1) + 2
= (x + 1)2 + 2 > 0 [ vì (x + 1)2 \(\ge\)0; 2 >0)
=> đa thức f(x) ko có nghiệm

a) f(x) = x(x - 5) + 2(x - 5)
x(x - 5) + 2(x - 5) = 0
<=> (x - 5)(x - 2) = 0
x - 5 = 0 hoặc x - 2 = 0
x = 0 + 5 x = 0 + 2
x = 5 x = 2
=> x = 5 hoặc x = 2
a, f(x) có nghiệm
\(\Leftrightarrow x\left(x-5\right)+2\left(x-5\right)=0\)
\(\Rightarrow\left(x-5\right)\left(x+2\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-5=0\\x+2=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=5\\x=-2\end{cases}}\)
->tự kết luận.
b1, để g(x) có nghiệm thì:
\(g\left(x\right)=2x\left(x-2\right)-x^2+5+4x=0\)
\(\Rightarrow2x^2-4x-x^2+5+4x=0\)
\(\Rightarrow x^2+5=0\)
Do \(x^2\ge0\forall x\)nên\(x^2+5\ge5\forall x\)
suy ra: k tồn tại \(x^2+5=0\)
Vậy:.....
b2,
\(f\left(x\right)=x\left(x-5\right)+2\left(x-5\right)\)
\(=x^2-5x+2x-10\)
\(=x^2-3x-10\)
\(f\left(x\right)-g\left(x\right)=x^2+5-\left(x^2-3x-10\right)\)
\(=x^2+5-x^2+3x-10=3x-5\)

a, \(4x+9\)
Để đa thức trên có nghiệm thì:
\(4x+9=0\Rightarrow x=\dfrac{-9}{4}\)
Vậy, ...
b, \(-5x+6\)
Để đa thức trên có nghiệm thì:
\(-5x+6=0\Rightarrow x=\dfrac{-6}{5}\)
Vậy, ...
c, \(x^2-1\)
Để đa thức trên có nghiệm thì:
\(x^2-1=0\Rightarrow x^2=1\Rightarrow x=\pm1\)
Vậy, ...
d, \(x^2-9\)
Để đa thức trên có nghiệm thì:
\(x^2-9=0\Rightarrow x^2=9\Rightarrow x=\pm3\)
e, \(x^2-x\)
Để đa thức trên có nghiệm thì:
\(x^2-x=0\Rightarrow x\left(x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy, ...
f, \(x^2-2x\)
Để đa thức trên có nghiệm thì:
\(x^2-2x=0\Rightarrow x\left(x-2\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Vậy, ...
g, \(x^2-3x\)
Để đa thức trên có nghiệm thì:
\(x^2-3x=0\Rightarrow x\left(x-3\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
Vậy, ...
h, \(3x^2-4x\)
Để đa thức trên có nghiệm thì:
\(3x^2-4x=0\Rightarrow x\left(3x-4\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{4}{3}\end{matrix}\right.\)
Vậy, ...
vâng ạ
Đề sai rồi bạn