Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
+) TXĐ: D = R
+) Ta có đạo hàm y’ = ( x2 - 2( m + 3) x + 4) .ex .
Hàm số nghịch biến trên TXĐ khi y’ = ( x2 - 2( m + 3) x + 4) .ex ≤ 0 mọi x


\(y'=\left(2m+1\right)\cos x+3-m\)
Hàm số đã cho đồng biến trên R \(\Leftrightarrow y'\ge0,\forall x\in R\)
\(\Leftrightarrow\left(2m+1\right)\cos x\le m-3\) (1)
*TH: \(2m+1< 0\Leftrightarrow m< \frac{-1}{2}\), ta có
\(\left(1\right)\Leftrightarrow\cos x\ge\frac{m-3}{2m+1}\) (không thoả với mọi x)
*TH: \(2m+1>0\Leftrightarrow m>\frac{-1}{2}\), ta có
\(\left(1\right)\Leftrightarrow\cos x\le\frac{m-3}{2m+1}\) (2)
(2) đúng với mọi x khi và chỉ khi \(\left|\frac{m-3}{2m+1}\right|>1\Leftrightarrow\left[\begin{array}{nghiempt}m< -4\\m>\frac{2}{3}\end{array}\right.\)
kết hợp \(m>\frac{-1}{2}\) ta có m > 3/2 là giá trị cần tìm

Theo mình:
để hàm số đồng biến, đk cần là y'=0.
a>0 và \(\Delta'< 0\)
nghịch biến thì a<0
vì denta<0 thì hầm số cùng dấu với a
mình giải được câu a với b
câu c có hai cực trị thì a\(\ne\)0, y'=0, denta>0 (để hàm số có hai nghiệm pb)
câu d dùng viet
câu e mình chưa chắc lắm ^^

a/ \(y'=x^2-mx-2\)
Để hàm số đồng biến trên R \(\Leftrightarrow y'\ge0\) \(\forall x\in R\)
\(\Leftrightarrow\Delta=m^2+8< 0\) (vô lý)
Vây không tồn tại m thỏa mãn
b/ \(y=\frac{x^2-2mx-1}{x-1}\Rightarrow y'=\frac{\left(2x-2m\right)\left(x-1\right)-\left(x^2-2mx-1\right)}{\left(x-1\right)^2}\)
\(y'=\frac{x^2-2x+2m+1}{\left(x-1\right)^2}=\frac{\left(x-1\right)^2+2m}{\left(x-1\right)^2}\)
Để hàm số đồng biến trên TXĐ
\(\Leftrightarrow y'\ge0\) \(\forall x\in D\Leftrightarrow\frac{\left(x-1\right)^2+m}{\left(x-1\right)^2}\ge0\) \(\forall x\Rightarrow m\ge0\)
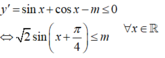
2.
\(y'=1+\left(m+1\right)cosx\le0;\forall x\in R\)
\(\Leftrightarrow\left(m+1\right)cosx\le-1\) ; \(\forall x\in R\)
- Với \(m=-1\) không thỏa mãn
- Với \(m>-1\Leftrightarrow cosx\le-\frac{1}{m+1}\)
\(\Rightarrow-\frac{1}{m+1}\ge1\Leftrightarrow m+1\le-1\Rightarrow m\le-2\) (ktm)
- Với \(m< -1\Leftrightarrow cosx\ge-\frac{1}{m+1}\Rightarrow-\frac{1}{m+1}\le-1\)
\(\Leftrightarrow m+1\ge1\Rightarrow m\ge0\) (ktm)
Vậy không tồn tại m để hàm đồng biến trên TXĐ
1.
\(y'=\left(2m+3\right)cosx+2-m\ge0;\forall x\)
\(\Leftrightarrow\left(2m+3\right)cosx\ge m-2\)
- Với \(m=-\frac{3}{2}\) thỏa mãn
- Với \(m>-\frac{3}{2}\Rightarrow cosx\ge\frac{m-2}{2m+3}\)
\(\Rightarrow\frac{m-2}{2m+3}\le\min\limits_Rcosx=-1\) \(\Leftrightarrow3m\le-1\Rightarrow m\le-\frac{1}{3}\Rightarrow-\frac{3}{2}< m\le-\frac{1}{3}\)
- Với \(m< -\frac{3}{2}\Rightarrow cosx\le\frac{m-2}{2m+3}\Rightarrow\frac{m-2}{2m+3}\ge\max\limits_Rcosx=1\)
\(\Leftrightarrow m-2\le2m+3\Rightarrow m\ge-5\)
Kết hợp lai ta được \(-5\le m\le-\frac{1}{3}\)