Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ta tính \(y'=3x^2-6x-m\)
để hàm số đồng biến trên R thì y'>0 với mọi x thuộc R
mà ta có \(y'=3x^2-6x-m\)>0 khi và chỉ khi \(\Delta=b^2-4ac<0\) do hệ số a của y' >0
mà \(\Delta=6^2+12m=36+12m<0\Rightarrow m<-3\)
vậy với m<-3 thì hàm số đồng biến trên R
a) Tập xác định: D = R\{m}
Hàm số đồng biến trên từng khoảng (−∞;m),(m;+∞)(−∞;m),(m;+∞)khi và chỉ khi:
y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2
b) Tập xác định: D = R\{m}
Hàm số nghịch biến trên từng khoảng khi và chỉ khi:
y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0
[m<1m>4[m<1m>4
c) Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3
d) Tập xác định: D = R
Hàm số đồng biến trên R khi và chỉ khi:
y′=3x2−4mx+12≥0⇔′=4m2−36≤0⇔m2≤9⇔−3≤m≤3
. Tập xác định : R 
{
} ;
và 
;
) ∈ ∆ ⇔ 
.
Bài 1:
Hàm đồng biến khi mà \(y'=x^2-2mx-2\geq 0\forall x\in\mathbb{R}\)
\(\Leftrightarrow \Delta'=m^2+2\leq 0\). Điều này vô lý nên không tồn tại $m$ thỏa mãn
Bài 2:
Hàm đồng biến khi mà \(y'=-\frac{4x^2+4x+3+2m}{(2x+1)^2}\geq 0\) với mọi $x$ thuộc TXĐ
\(\Leftrightarrow 4x^2+4x+3+2m\leq 0\forall x\in\mathbb{R}\setminus \frac{-1}{2}\)
\(\Leftrightarrow m\leq -2(x^2+2x+1,5)\Leftrightarrow m\leq \min (-2x^2-2x-1,5)\)
Điều này vô lý vì không tồn tại min của \(-2x^2-2x-1,5\forall x\in\mathbb{R}\setminus\frac{-1}{2}\)
Vậy không tồn tại $m$ thỏa mãn.
nên từ đồ thị (C) ta suy ra ngay đồ thị của hàm số :
\(y=\left|\dfrac{x^3}{6}+\dfrac{3x^2}{2}+\dfrac{5x}{2}\right|\) là hình 18
Ta có : \(y'=\frac{m^2-4}{\left(x-m\right)^2},x\ne m\) nên hàm số (1) đồng biến trên khoảng (-\(\infty\);3] khi và chỉ khi \(\begin{cases}y'>0,x\in\left(-\infty;3\right)\\m\notin\left(-\infty;3\right)\end{cases}\)\(\begin{cases}m^2-4>0\\m>3\end{cases}\)
\(\Leftrightarrow\)m<-2 hoặc m>2 và m>3 <=> m>3
Vậy m>3 thì hàm số đồng biến trên khoảng (-\(\infty\);3]
Lời giải + diễn giải
để hàm có cực trị f'(x) phải có nghiệm và đổi dấu qua nghiệm
a) \(y'=3x^2-6x+m\)
xét f(x)= 3x^2 -6x+m
để f(x) là hàm bậc 2 => có nghiệm và đổi dấu qua nghiệm đk cần và đủ \(\Delta>0\)
\(\Leftrightarrow\Delta'=9-3m>0\Rightarrow m< 3\)
Kết luận với m< 3 hàm A(x) luôn có cực trị
b)
\(y'=3x^2+4mx+m\)
\(\Delta'=4m^2-3m>0\Leftrightarrow\left[{}\begin{matrix}m< 0\\m>\dfrac{3}{4}\end{matrix}\right.\)
c)
\(y=\dfrac{x^2-2mx+5}{x-m}\Rightarrow\left\{{}\begin{matrix}x\ne m\\y=\left(x-m\right)+\dfrac{5-m^2}{x-m}\end{matrix}\right.\)
\(y'=1+\dfrac{m^2-5}{\left(x-m\right)^2}\)
\(y'=0\Leftrightarrow\left(x-m\right)^2+m^2-5=0\Rightarrow5-m^2>0\Rightarrow-\sqrt{5}< m< \sqrt{5}\)
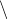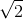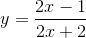y'=\(\dfrac{m\left(3x-m+1\right)-\left(mx+5\right)\cdot3}{\left(3x-m+1\right)^2}=\dfrac{-m^2+m-15}{\left(3x-m+1\right)^2}\)
Để y đồng biến trên R thì y'\(\ge\)0 <=>-m2+m-15\(\ge\)0(do mẫu luôn lớn hơn hoặc bằng 0
Mà
-m2+m-15\(=-\dfrac{59}{4}-\left(m-\dfrac{1}{2}\right)^2< 0\)với mọi m
=>không tồn tại m để y luôn đồng biến