
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:\(x^3y^5+3x^3y^5+5x^3y^5+...+\left(2k-1\right)x^3y^5=3249x^3y^5\)
\(x^3y^5\left(1+3+5+...+2k-1\right)=3249x^3y^5\)
\(\Rightarrow1+3+5+...+2k-1=3249\)
\(\Rightarrow\frac{\left(\frac{2k-1-1}{2}+1\right).\left(2k-1+1\right)}{2}=3249\)
\(\Rightarrow\frac{k.2k}{2}=3249\)
\(\Rightarrow k^2=3249\)
\(\Rightarrow k=57\) hoặc k=-57

Nhìn biểu thức có vẻ rối, nhưng ta chẳng cần quan tâm cái biến làm gì cả.
Coi như không có biến, ta có :
\(1+3+5+...+\left(2k-1\right)=3249\)
\(\Rightarrow\dfrac{\dfrac{\left(2k-1\right)-1}{2}+1}{2}\cdot\left(2x-1+1\right)=3249\)
\(\Rightarrow CALC\left(k\right)=57\)
Vậy \(k=57\)



a) Ta có: \(\left|2x-5\right|\ge0\forall x\)
\(\left|3y+1\right|\ge0\forall y\)
Do đó: \(\left|2x-5\right|+\left|3y+1\right|\ge0\forall x,y\)
mà \(\left|2x-5\right|+\left|3y+1\right|=0\)
nên \(\left\{{}\begin{matrix}\left|2x-5\right|=0\\\left|3y+1\right|=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-5=0\\3y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=5\\3y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\frac{5}{2}\\y=\frac{-1}{3}\end{matrix}\right.\)
Vậy: \(x=\frac{5}{2}\) và \(y=\frac{-1}{3}\)
b) Ta có: \(\left|3x-4\right|\ge0\forall x\)
\(\left|3y-5\right|\ge0\forall y\)
Do đó: \(\left|3x-4\right|+\left|3y-5\right|\ge0\forall x,y\)
mà \(\left|3x-4\right|+\left|3y-5\right|=0\)
nên \(\left\{{}\begin{matrix}\left|3x-4\right|=0\\\left|3y-5\right|=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-4=0\\3y-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=4\\3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\frac{4}{3}\\y=\frac{5}{3}\end{matrix}\right.\)
Vậy: \(x=\frac{4}{3}\) và \(y=\frac{5}{3}\)
c) Ta có: |16-|x||≥0∀x
\(\left|5y-2\right|\ge0\forall y\)
Do đó: |16-|x||+|5y-2|≥0∀x,y
mà |16-|x||+|5y-2|=0
nên \(\left\{{}\begin{matrix}\text{|16-|x||}=0\\\left|5y-2\right|=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}16-\left|x\right|=0\\5y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left|x\right|=16\\5y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{16;-16\right\}\\y=\frac{2}{5}\end{matrix}\right.\)
Vậy: \(x\in\left\{16;-16\right\}\) và \(y=\frac{2}{5}\)

có |2x-5| luôn \(\ge0\forall x\in Q\)
cũng có \(\left|3y+1\right|\ge0\forall y\in Q\)
=> \(\left|2x-5\right|+\left|3y-1\right|\ge0\forall x;y\in Q\)
=>\(\hept{\begin{cases}2x-5=0\\3y-1=0\end{cases}}\)<=> \(\hept{\begin{cases}2x=5\\3y=1\end{cases}}\)<=> \(\hept{\begin{cases}x=\frac{2}{5}\\y=\frac{1}{3}\end{cases}}\)
vậy \(x=\frac{2}{5};y=\frac{1}{3}\)
em nhớ là phải dùng ngoặc nhọn như trên nhé! Nếu không sẽ sai đấy!
3 câu còn lại cũng tương tự
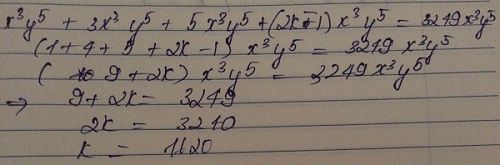
\(x^3y^5+3x^3y^5+...+\left(2k-1\right)x^3y^5=3249x^3y^5\)
\(\Leftrightarrow x^3y^5\left[1+2+3+...+\left(2k-1\right)\right]=3249x^3y^5\)
\(\Leftrightarrow1+3+5+...+\left(2k-1\right)=3249\)
\(\Leftrightarrow\frac{\left[\left(2k-1\right)+1\right].\left(\frac{\left(2k-1\right)-1}{2}+1\right)}{2}=3249\)
\(\Leftrightarrow\frac{2k.\left(k-1+1\right)}{2}=3249\)
\(\Leftrightarrow\frac{2k^2}{2}=3249\)
\(\Leftrightarrow k^2=3249=57^2\) ( ko xét k = - 57 vì theo quy luật thi k luôn dương )
\(\Rightarrow k=57\)
kết quả k = 57