Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\dfrac{x}{2}=\dfrac{y}{5}vàx+y=-21\)
Ta có:\(\dfrac{x}{2}=\dfrac{y}{5}\Rightarrow\dfrac{x+y}{2+5}=\dfrac{-21}{7}=-3\)
\(\Rightarrow\dfrac{x}{2}=-3\Rightarrow x=\left(-3\right).2=-6\)
\(\dfrac{y}{5}=-3\Rightarrow y=\left(-3\right).5=-15\)
Ta có: \(\dfrac{x}{2}=\dfrac{y}{5}\) ( x,y \(\in\) Q )
Áp dụng tính chất tỉ lệ thức:
\(\dfrac{x}{2}=\dfrac{y}{5}\)\(=\dfrac{x+y}{2+5}=\dfrac{-21}{7}=-3\)
\(\Rightarrow\left\{{}\begin{matrix}x=2.\left(-3\right)=-6\\y=5.\left(-3\right)=-15\end{matrix}\right.\)
Đặt k = 
. Ta có x = 2k, y = 5k
Từ xy=10. suy ra 2k.5k = 10 => 10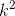 
= 10 => 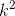= 1 => k = ± 1
Với k = 1 ta được = 1 suy ra x = 2, y = 5
Với k = -1 ta được = -1 suy ra x = -2, y = -5
Gọi \(\dfrac{x}{2}=\dfrac{y}{5}=k\)
Với \(\dfrac{x}{2}=k\Rightarrow x=2k\); \(\dfrac{y}{5}=k\Rightarrow y=5k\)
Theo đề bài,ta còn có:
\(xy=10\)
hay 2k.5k=10
10k2 =10
\(\Rightarrow k=\pm1\)
Với k=1 \(\Rightarrow\dfrac{x}{2}=\dfrac{y}{5}=1\Rightarrow x=2;y=5\)
Với k=-1 \(\Rightarrow\dfrac{x}{2}=\dfrac{y}{5}=-1\Rightarrow x=-2;y=-5\)
a) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{7}=\dfrac{y}{13}=\dfrac{x+y}{7+13}=\dfrac{40}{20}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=7.2=14\\y=13.2=26\end{matrix}\right.\)
Vật \(x=14;y=26\)
b) (Chỗ này bạn viết nhầm thì phải)
Ta có:
\(7x=3y\Rightarrow\dfrac{x}{3}=\dfrac{y}{7}\)
và \(x-y=-16\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3}=\dfrac{y}{7}=\dfrac{x-y}{3-7}=\dfrac{-16}{-4}=4\)
\(\Rightarrow\left\{{}\begin{matrix}x=3.4=12\\y=7.4=28\end{matrix}\right.\)
Vậy \(x=12;y=28\)
c) Ta có:
\(\dfrac{x}{19}=\dfrac{y}{21}=\dfrac{2x}{38}\)
và \(2x-y=34\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{2x}{38}=\dfrac{y}{21}=\dfrac{2x-y}{38-21}=\dfrac{34}{17}=2\)
\(\Rightarrow\left\{{}\begin{matrix}2x=38.2=76\Rightarrow x=38\\y=21.2=42\end{matrix}\right.\)
Vậy \(x=38;y=42\)
d) Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{9+16}=\dfrac{100}{25}=4\)
\(\Rightarrow\left\{{}\begin{matrix}x^2=9.4=36=6^2=\left(-6\right)^2\Rightarrow\left[{}\begin{matrix}x=6\\x=-6\end{matrix}\right.\\y^2=16.4=64=8^2=\left(-8\right)^2\Rightarrow\left[{}\begin{matrix}y=8\\y=-8\end{matrix}\right.\end{matrix}\right.\)
Vậy \(\left(x:y\right)\in\left\{\left(6;8\right);\left(6;-8\right);\left(-6;8\right);\left(-6;-8\right)\right\}\)
Cả 4 cái có 1 câu huyền thoại:"Áp dụng tính chất dãy tỉ số = nhau ta có" nên mk nói cho cả 4 lun :v
a) \(\dfrac{x}{7}=\dfrac{y}{13}=\dfrac{x+y}{7+13}=\dfrac{40}{20}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=2.7=14\\y=2.13=26\end{matrix}\right.\)
b) \(\dfrac{x}{19}=\dfrac{y}{21}\Rightarrow\dfrac{2x}{38}=\dfrac{y}{21}=\dfrac{2x-y}{38-21}=\dfrac{34}{17}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=2.19=38\\y=2.21=42\end{matrix}\right.\)
c) \(7x=3y\Rightarrow\dfrac{x}{3}=\dfrac{y}{7}=\dfrac{x-y}{3-7}=\dfrac{-16}{-4}=4\)
\(\Rightarrow\left\{{}\begin{matrix}x=4.3=12\\y=4.7=28\end{matrix}\right.\)
c) \(\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{9+16}=\dfrac{100}{25}=4\)
\(\Rightarrow\left\{{}\begin{matrix}x^2=4.9=36\Rightarrow x=\pm6\\y^2=4.16=64\Rightarrow y=\pm8\end{matrix}\right.\)
\(\)
Lời giải:
Theo tính chất của dãy tỉ số bằng nhau ta có:
Do đó
Vậy x=6, y =10
a)\(\dfrac{x}{8}=\dfrac{y}{5}=\dfrac{z}{12}\Leftrightarrow\dfrac{-x}{-8}=\dfrac{y}{5}=\dfrac{z}{12}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{-x}{-8}=\dfrac{y}{5}=\dfrac{z}{12}=\dfrac{-x+y+z}{-8+5+12}=\dfrac{60}{9}=\dfrac{20}{3}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{20}{3}.8=\dfrac{160}{3}\\y=\dfrac{20}{3}.5=\dfrac{100}{3}\\z=\dfrac{20}{3}.12=80\end{matrix}\right.\)
b) \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\Leftrightarrow\dfrac{x}{2}=\dfrac{2y}{6}=\dfrac{3z}{12}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{2}=\dfrac{2y}{6}=\dfrac{3z}{12}=\dfrac{x+2y-3z}{2+6-12}=\dfrac{-20}{-4}=5\)
\(\Rightarrow\left\{{}\begin{matrix}x=5.2=10\\y=5.3=15\\z=5.4=20\end{matrix}\right.\)
c) \(\left\{{}\begin{matrix}4x=3y\\7y=5z\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=\dfrac{y}{4}\\\dfrac{y}{5}=\dfrac{z}{7}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{15}=\dfrac{y}{20}\\\dfrac{y}{20}=\dfrac{z}{28}\end{matrix}\right.\) \(\Leftrightarrow\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}=\dfrac{x-y+z}{15-20+28}=\dfrac{-46}{23}=-2\)
\(\Rightarrow\left\{{}\begin{matrix}x=-2.15=-30\\y=-2.20=-40\\z=-2.28=-56\end{matrix}\right.\)
Ta có \(\frac{x+5}{2}=\frac{y-2}{3}\)và \(x-y=-10\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x+5}{2}=\frac{y-2}{3}=\frac{x+5-y-2}{2-3}=\frac{x-y+5-2}{2-3}=\frac{-10+5-2}{2-3}=\frac{-7}{-1}=7\)
=> \(\frac{x+5}{2}=7\)=> x + 5 = 14 => x = 9
và \(\frac{y-2}{3}=7\)=> y - 2 = 21 => y = 23
Ta có:\(\frac{3}{5}x=\frac{2}{3}y\)
\(\Leftrightarrow\left(\frac{3}{5}x\right)^2=\left(\frac{2}{3}y\right)^2\)
\(\Leftrightarrow\frac{9}{25}x^2=\frac{4}{9}y^2\left(2\right)\)
Mà \(x^2-y^2=38\Rightarrow x^2=38+y^2\left(1\right)\)
Lấy (1) thay vào (2) ta đc:\(\frac{9}{25}\left(38+y^2\right)=\frac{4}{9}y^2\)
\(\Leftrightarrow\frac{342}{25}+\frac{9}{25}y^2-\frac{4}{9}y^2=0\)
\(\Leftrightarrow\frac{19}{225}y^2=\frac{342}{25}\)
\(\Leftrightarrow\)\(y=\sqrt{162}\)
Ko bt có đúng ko mong bn kiểm tra lại rồi nói với mk
Câu 1 :
a. Theo đề bài ta có :
\(\dfrac{x}{2}=\dfrac{y}{5}\) và \(x+y=21\)
Áp dụng t/c dãy tỉ số bằng nhau :
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{21}{7}=3\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{2}=3\Rightarrow x=2.3=6\\\dfrac{y}{5}=3\Rightarrow y=3.5=15\end{matrix}\right.\)
Vậy..............
b. Đặt \(\dfrac{x}{2}=\dfrac{y}{3}=k\Leftrightarrow\left\{{}\begin{matrix}2k\\3y\end{matrix}\right.\)
mà \(x.y=54\)
hay \(2k.3k=54\)
\(\Rightarrow6.k^2=54\)
\(\Rightarrow k^2=9=\left(\pm3\right)^2\)
Với \(k=3\Rightarrow\left\{{}\begin{matrix}x=2.3=6\\y=3.3=9\end{matrix}\right.\)
Với \(k=-3\Rightarrow\left\{{}\begin{matrix}x=\left(-3\right).2=-6\\y=\left(-3\right).3=-9\end{matrix}\right.\)
Vậy..............
c. Áp dụng t/c dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{7}=\dfrac{y}{5}=\dfrac{x-y}{7-5}=\dfrac{12}{2}=6\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{7}=6\Rightarrow x=7.6=42\\\dfrac{y}{5}=6\Rightarrow y=5.6=40\end{matrix}\right.\)
Vậy............
a, \(\frac{2}{3}x=\frac{3}{4}y=\frac{4}{5}z\)
\(\Rightarrow\frac{2x}{3.12}=\frac{3y}{4.12}=\frac{4z}{5.12}\)
\(\Rightarrow\frac{x}{18}=\frac{y}{16}=\frac{z}{15}=\frac{x+y+z}{18+16+15}=\frac{45}{49}\)
Đến đây tự làm tiếp nhé
b, \(2x=3y=5z\Rightarrow\frac{2x}{30}=\frac{3y}{30}=\frac{5z}{30}\Rightarrow\frac{x}{15}=\frac{y}{10}=\frac{z}{6}=\frac{x+y-z}{15+10-6}=\frac{95}{19}=5\)
=> x = 75, y = 50, z = 30
c, \(\frac{3}{4}x=\frac{5}{7}y=\frac{10}{11}z\)
\(\Rightarrow\frac{3x}{4.30}=\frac{5y}{7.30}=\frac{10z}{11.30}\)
\(\Rightarrow\frac{x}{40}=\frac{y}{42}=\frac{z}{33}\)
\(\Rightarrow\frac{2x}{80}=\frac{3y}{126}=\frac{4z}{132}=\frac{2x-3y+4z}{80-126+132}=\frac{8,6}{86}=\frac{1}{10}\)
=> x=... , y=... , z=...
d, Đặt \(\frac{x}{2}=\frac{y}{5}=k\Rightarrow x=2k,y=5k\)
Ta có: xy = 90 => 2k.5k = 90 => 10k2 = 90 => k2 = 9 => k = 3 hoặc -3
Với k = 3 => x = 6, y = 15
Với k = -3 => x = -6, y = -15
Vậy...
e, Tương tự câu d
b) Ta có :\(\text{ 2x = 3y = 5z }=\frac{x}{\frac{1}{2}}=\frac{y}{\frac{1}{3}}=\frac{z}{\frac{1}{5}}=\frac{x+y-z}{\frac{1}{2}+\frac{1}{3}-\frac{1}{5}}=\frac{95}{\frac{19}{30}}=\frac{1}{6}\)
=> \(2x=\frac{1}{6}\Rightarrow x=\frac{1}{12}\)
\(3y=\frac{1}{6}\Rightarrow y=\frac{1}{18}\)
\(5z=\frac{1}{6}\Rightarrow z=\frac{1}{30}\)
\(x=-6;x=-15.\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{2}\)=\(\dfrac{y}{5}\)=\(\dfrac{x+y}{2+5}\)=\(\dfrac{-21}{7}\)=-3
=>\(\dfrac{x}{2}\)=\(\dfrac{y}{5}\)=5x=2y
=>x=5.-3=-15
=>y=2.-3=-6
Vậy x=-15;y=6