Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
Tìm max:
Áp dụng BĐT Bunhiacopxky ta có:
\(y^2=(3\sqrt{x-1}+4\sqrt{5-x})^2\leq (3^2+4^2)(x-1+5-x)\)
\(\Rightarrow y^2\leq 100\Rightarrow y\leq 10\)
Vậy \(y_{\max}=10\)
Dấu đẳng thức xảy ra khi \(\frac{\sqrt{x-1}}{3}=\frac{\sqrt{5-x}}{4}\Leftrightarrow x=\frac{61}{25}\)
Tìm min:
Ta có bổ đề sau: Với $a,b\geq 0$ thì \(\sqrt{a}+\sqrt{b}\geq \sqrt{a+b}\)
Chứng minh:
\(\sqrt{a}+\sqrt{b}\geq \sqrt{a+b}\)
\(\Leftrightarrow (\sqrt{a}+\sqrt{b})^2\geq a+b\)
\(\Leftrightarrow \sqrt{ab}\geq 0\) (luôn đúng).
Dấu "=" xảy ra khi $ab=0$
--------------------
Áp dụng bổ đề trên vào bài toán ta có:
\(\sqrt{x-1}+\sqrt{5-x}\geq \sqrt{(x-1)+(5-x)}=2\)
\(\sqrt{5-x}\geq 0\)
\(\Rightarrow y=3(\sqrt{x-1}+\sqrt{5-x})+\sqrt{5-x}\geq 3.2+0=6\)
Vậy $y_{\min}=6$
Dấu "=" xảy ra khi \(\left\{\begin{matrix} (x-1)(5-x)=0\\ 5-x=0\end{matrix}\right.\Leftrightarrow x=5\)
Bài 2:
\(A=\sqrt{(x-1994)^2}+\sqrt{(x+1995)^2}=|x-1994|+|x+1995|\)
Áp dụng BĐT dạng \(|a|+|b|\geq |a+b|\) ta có:
\(A=|x-1994|+|x+1995|=|1994-x|+|x+1995|\geq |1994-x+x+1995|=3989\)
Vậy \(A_{\min}=3989\)
Đẳng thức xảy ra khi \((1994-x)(x+1995)\geq 0\Leftrightarrow -1995\leq x\leq 1994\)

1)???
2) \(A=\dfrac{3x^2-8x+6}{x^2-2x+1}=2+\dfrac{x^2-4x+4}{x^2-2x+1}=2+\dfrac{\left(x-2\right)^2}{\left(x-1\right)^2}\ge2\)
Vậy GTNN của A là 2 tại x=2.
3) \(\)Đặt \(a=\dfrac{1}{x+100}\Rightarrow x=\dfrac{1}{a}-100\)
\(D=\dfrac{x}{\left(x+100\right)^2}=a^2x=a^2\left(\dfrac{1}{a}-100\right)=a-100a^2=-100\left(a^2-\dfrac{a}{100}+\dfrac{1}{40000}-\dfrac{1}{40000}\right)=-100\left(a-\dfrac{1}{200}\right)^2+\dfrac{1}{400}\le\dfrac{1}{400}\)
Vậy GTLN của D là \(\dfrac{1}{400}\) tại \(a=\dfrac{1}{200}\Leftrightarrow x=100\)

a) \(M=\left(\dfrac{x^2-1}{x^4-x^2+1}-\dfrac{1}{x^2+1}\right).\left(x^4+\dfrac{1-x^4}{1+x^2}\right)\)
\(M=\left(\dfrac{(x^2-1)\left(x^2+1\right)-\left(x^4-x^2+1\right)}{(x^4-x^2+1)\left(x^2+1\right)}\right).\left(\dfrac{x^6+x^4+1-x^4}{1+x^2}\right)\)
\(M=\left(\dfrac{x^4-1-\left(x^4-x^2+1\right)}{x^6+1}\right).\left(\dfrac{x^6+1}{1+x^2}\right)\)
\(M=\left(\dfrac{x^2-2}{x^6+1}\right).\left(\dfrac{x^6+1}{1+x^2}\right)\)
\(M=\dfrac{x^2-2}{x^2+1}\)
b) Ta có:
\(x^2\ge0\left(\forall x\right)\)
\(x^2-2\ge-2\)
\(\dfrac{x^2-2}{x^2+1}\ge-2\)
do mẫu \(x^2+1\) lớn hơn 0 nên chia ko cần đổi dấu
\(\Rightarrow M\ge-2\)


a: \(A=\dfrac{x-2-2x-4+x}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{-\left(x-2\right)\left(x+1\right)}{6\left(x+2\right)}\)
\(=\dfrac{-6}{\left(x+2\right)}\cdot\dfrac{-\left(x+1\right)}{6\left(x+2\right)}=\dfrac{\left(x+1\right)}{\left(x+2\right)^2}\)
b: A>0
=>x+1>0
=>x>-1
c: x^2+3x+2=0
=>(x+1)(x+2)=0
=>x=-2(loại) hoặc x=-1(loại)
Do đó: Khi x^2+3x+2=0 thì A ko có giá trị


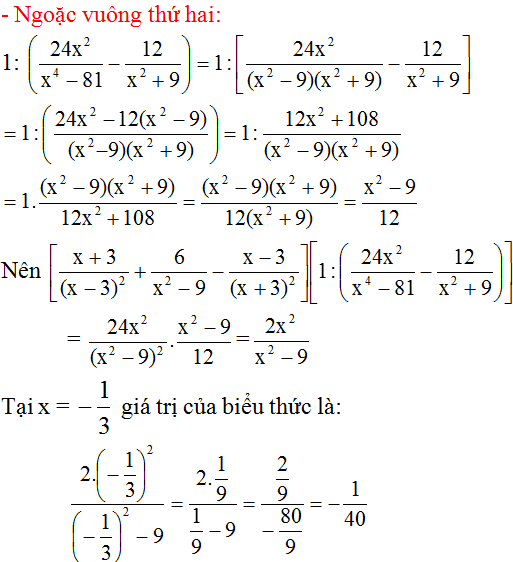


\(D=\dfrac{x^2}{x-2}\left(\dfrac{x^2+4-4x}{x}\right)+3\)
\(D=\dfrac{x^2}{x-2}\dfrac{\left(x-2\right)^2}{x}+3\)
\(D=x\left(x-2\right)+3\)
\(D=x^2-2x+1+2\)
\(D=\left(x-1\right)^2+2\ge2\)
Dấu"=" xảy ra \(\Leftrightarrow\left(x-1\right)^2=0\)
\(\Leftrightarrow x=1\)
Vậy MinD là 2 \(\Leftrightarrow x=1\)