
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/ \(M=x^2-2.\frac{3}{2}x+\left(\frac{3}{2}\right)^2-\left(\frac{3}{2}\right)^2+5\)
\(=\left(x-\frac{3}{2}\right)^2+\frac{11}{4}\ge\frac{11}{4}\)
Vậy Min M = 11/4 khi x - 3/2 = 0 => x = 3/2
b/ \(N=-\left(4x^2-\frac{2}{8}x+5\right)\)
\(=-\left[\left(2x\right)^2-2.2x.\frac{1}{16}+\left(\frac{1}{16}\right)^2-\left(\frac{1}{16}\right)^2+5\right]\)
\(=-\left(2x-\frac{1}{16}\right)^2-\frac{1279}{256}\ge-\frac{1279}{256}\)
Vậy Min N = -1279/256 khi 2x - 1/16 = 0 => 2x = 1/16 => x = 1/32

a)\(A=4x^2+4x+11\)
\(=4x^2+4x+1+10\)
\(=\left(2x+1\right)^2+10\ge10\)
Dấu = khi \(x=\frac{-1}{2}\)
Vậy MinA=10 khi \(x=\frac{-1}{2}\)
b)\(B=3x^2-6x+1\)
\(=3x^2-6x+3-2\)
\(=3\left(x^2-2x+1\right)-2\)
\(=3\left(x-1\right)^2-2\ge-2\)
Dấu = khi \(x=1\)
Vậy MinB=-2 khi \(x=1\)
c)\(C=x^2-2x+y^2-4y+6\)
\(=\left(x^2-2x+1\right)+\left(y^2-4y+4\right)+1\)
\(=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\)
Dấu = khi \(\hept{\begin{cases}x=1\\y=-2\end{cases}}\)
Vậy MinC=1 khi \(\hept{\begin{cases}x=1\\y=-2\end{cases}}\)

\(A=2x^2+y^2+2xy-6x-2y+10\)
\(=\left(\left(x^2+2xy+y^2\right)-2\left(x+y\right)+1\right)+\left(x^2-4x+4\right)+5\)
\(=\left(x+y-1\right)^2+\left(x-2\right)^2+5\ge5\)
Vậy GTNN là A = 5 khi \(\hept{\begin{cases}x=2\\y=-1\end{cases}}\)

\(\left(\text{*}\right)\) Tìm giá trị lớn nhất của biểu thức sau:
Ta có:
\(A=\frac{x^2+1}{x^2-x+1}=\frac{2\left(x^2-x+1\right)-\left(x^2-2x+1\right)}{x^2-x+1}=2-\frac{\left(x-1\right)^2}{x^2-x+1}\le2\) với mọi \(x\)
Dấu \("="\) xảy ra \(\Leftrightarrow\) \(\left(x-1\right)^2=0\) \(\Leftrightarrow\) \(x-1=0\) \(\Leftrightarrow\) \(x=1\)
Vậy, \(A_{max}=2\) \(\Leftrightarrow\) \(x=1\)
-------------------------------------------------
\(B=\frac{3-4x}{x^2+1}=\frac{4\left(x^2+1\right)-\left(4x^2+4x+1\right)}{x^2+1}=4-\frac{\left(2x+1\right)^2}{x^2+1}\le4\) với mọi \(x\)
Dấu \("="\) xảy ra \(\Leftrightarrow\) \(\left(2x+1\right)^2=0\) \(\Leftrightarrow\) \(2x+1=0\) \(\Leftrightarrow\) \(x=-\frac{1}{2}\)
Vậy, \(B_{max}=4\) \(\Leftrightarrow\) \(x=-\frac{1}{2}\)
____________________________________
\(\left(\text{*}\text{*}\right)\) Tìm giá trị nhỏ nhất của biểu thức sau:
Từ \(A=\frac{x^2+1}{x^2-x+1}\)
\(\Rightarrow\) \(3A=\frac{3x^2+3}{x^2-x+1}=\frac{\left(x^2+2x+1\right)+2\left(x^2-x+1\right)}{x^2-x+1}=\frac{\left(x+1\right)^2}{x^2-x+1}+2\ge2\) với mọi \(x\)
Vì \(3A\ge2\) nên \(A\ge\frac{2}{3}\)
Dấu \("="\) xảy ra \(\Leftrightarrow\) \(\left(x+1\right)^2=0\) \(\Leftrightarrow\) \(x+1=0\) \(\Leftrightarrow\) \(x=-1\)
Vậy, \(A_{min}=\frac{2}{3}\) \(\Leftrightarrow\) \(x=-1\)
Câu b) tự giải

-x^2+6x-11
=-(x^2-6x+11)
=-(x^2-6x+9+2)
=-(x-3)^2-2<=-2
Dấu = xảy ra khi x=3

Ta có: \(x^2-2x+y^2-4y+7\)
\(=\left(x^2-2x+1\right)+\left(y^2-4y+4\right)+2\)
\(=\left(x-1\right)^2+\left(y-2\right)^2+2\)
Vì:\(\left(x-1\right)^2+\left(y-2\right)^2\ge0\forall x\)
\(\Rightarrow\left(x-1\right)^2+\left(y-2\right)^2+2\ge2\forall x\)
Dấu = xảy ra khi: \(\hept{\begin{cases}\left(x-1\right)^2=0\\\left(y-2\right)^2=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1\\y=2\end{cases}}\)
Vậy:GTNN của bt là 2 tại x=1,y=2

Lời giải:
a.
Tại $x=5$ thì $B=\frac{5+3}{5-2}=\frac{8}{3}$
b.
\(A=\frac{x^2-x+1}{(x-2)(x+2)}+\frac{2(x+2)}{(x-2)(x+2)}-\frac{x-2}{(x-2)(x+2)}=\frac{x^2-x+1+2(x+2)-(x-2)}{(x-2)(x+2)}\)
\(=\frac{x^2+7}{(x-2)(x+2)}\)
c.
\(P=A:B(x+2)=\frac{x^2+7}{(x-2)(x+2)}:\frac{x+3}{x-2}.(x+2)=\frac{x^2+7}{x+3}\)
Áp dụng BĐT Cô-si:
$x^2+1\geq 2|x|\geq 2x$
$\Rightarrow x^2+7\geq 2x+6=2(x+3)$
$\Rightarrow P\geq \frac{2(x+3)}{x+3}=2$
Vậy $P_{\min}=2$. Giá trị này đạt tại $x^2=1\Leftrightarrow x=\pm 1$ (tm)
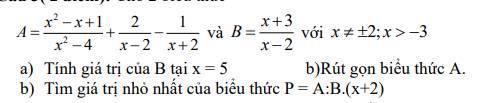
\(A=x^2-6x+11\)
\(\Leftrightarrow A=x^2-2.3x+9+2\)
\(\Leftrightarrow A=\left(x-3\right)^2+2\ge2\)
\(\Leftrightarrow A_{min}=2\)
\(\Leftrightarrow x-3=0\)
\(x=3\)