K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H
0
KN
9 tháng 9 2019
\(A=x^2-3x+1=x^2-2.\frac{3}{2}x+\frac{9}{4}-\frac{5}{4}\)
\(=\left(x-\frac{3}{2}\right)^2-\frac{5}{4}\ge\frac{-5}{4}\)
Vậy GTNN của A là \(\frac{-5}{4}\)\(\Leftrightarrow x=\frac{3}{2}\)
KN
9 tháng 9 2019
\(C=10x-x^2+2=-\left(x^2-10x-2\right)\)
\(=-\left(x^2-10x+25-27\right)=-\left[\left(x-5\right)^2-27\right]\)
\(=-\left(x-5\right)^2+27\le27\)
Vậy \(C_{max}=27\Leftrightarrow x=5\)
25 tháng 7 2016
4-8x-16x2= -16x2-8x -1 +5= -(16x2+8x+1)+5= -(4x+1)2+5 \(\le\)0+5=5
Dấu bằng xảy ra khi 4x-1 =0 tương đương với x=\(\frac{1}{4}\)
Vậy giá trị lớn nhất của bt là 5 khi và chỉ khi x = \(\frac{1}{4}\)
KN
23 tháng 8 2020
\(A=5-8x+x^2=-8x+x^2+6-11\)
\(=\left(x-4\right)^2-11\)
Vì \(\left(x-4\right)^2\ge0\forall x\)\(\Rightarrow\left(x-4\right)^2-11\ge-11\)
Dấu "=" xảy ra \(\Leftrightarrow\left(x-4\right)^2=0\Leftrightarrow x-4=0\Leftrightarrow x=4\)
Vậy Amin = - 11 <=> x = 4
KN
23 tháng 8 2020
\(B=\left(2-x\right)\left(x+4\right)=-x^2-2x+8\)
\(=-\left(x^2+2x+1\right)+9=-\left(x+1\right)^2+9\)
Vì \(\left(x+1\right)^2\ge0\forall x\)\(\Rightarrow-\left(x+1\right)^2+9\le9\)
Dấu "=" xảy ra \(\Leftrightarrow-\left(x+1\right)^2=0\Leftrightarrow x+1=0\Leftrightarrow x=-1\)
Vậy Bmax = 9 <=> x = - 1
NT
4
NT
21 tháng 10 2016
Tìm x y sao cho bt sau đạt giá trị nhỏ nhất
M=8x2+yy2—4xy—16x+17
YH
1
8 tháng 7 2019
\(C=4x^2-4xy+y^2+4x^2-16x+16+1\)
\(=\left(2x-y\right)^2+(2x-4)^2+1\ge1\forall x;y\in R\)
Dấu "=" xảy ra<=> 2x-y=0 và 2x-4=0
<=>2x-y=0 và x=2 <=>y=4 và x=
Vậy....
\(B=3x^2-12x+16\)
\(=x^2-12x+36+2x^2-20\)
\(=\left(x-6\right)^2+2x^2-20\ge-20\forall x\in R\)
Dấu "=" xảy ra <=> \(\left(x-6\right)^2=0\)và \(2x^2=0\)
<=>x1 =6 và x2 =0
Vậy....
HV
3
7 tháng 12 2014
\(=2x^2-8x+5\)
\(=2\left(x^2-4x+\frac{5}{2}\right)\)
\(=2\left(x^2-4x+4-\frac{3}{2}\right)\)
\(=2\left(x-2\right)^2-3\)
Vậy GTNN là -3 khi x=2
27 tháng 3 2018
=> 2(x^2-4x+4+1)=2(x-2)^2 +2
Nhận thấy 2(x-2)^2 > hoặc = 0
ĐTXR khi x=2 ... => Min =2
25 tháng 7 2016
a) A= x2 + 4x + 5
=x2+4x+4+1
=(x+2)2+1≥0+1=1
Dấu = khi x+2=0 <=>x=-2
Vậy Amin=1 khi x=-2
b) B= ( x+3 ) ( x-11 ) + 2016
=x2-8x-33+2016
=x2-8x+16+1967
=(x-4)2+1967≥0+1967=1967
Dấu = khi x-4=0 <=>x=4
Vậy Bmin=1967 <=>x=4
Bài 2:
a) D= 5 - 8x - x2
=-(x2+8x-5)
=21-x2+8x+16
=21-x2+4x+4x+16
=21-x(x+4)+4(x+4)
=21-(x+4)(x+4)
=21-(x+4)2≤0+21=21
Dấu = khi x+4=0 <=>x=-4
10 tháng 10 2017
Bài 1:
c)C=x2+5x+8
=x2+5x+\(\left(\dfrac{5}{2}\right)^2\)+\(\dfrac{7}{4}\)
=\(\left(x+\dfrac{5}{2}\right)^2\)+\(\dfrac{7}{4}\)\(\ge\dfrac{7}{4}\)
Vậy \(C_{min}=\dfrac{7}{4}\Leftrightarrow x=-\dfrac{5}{2}\)
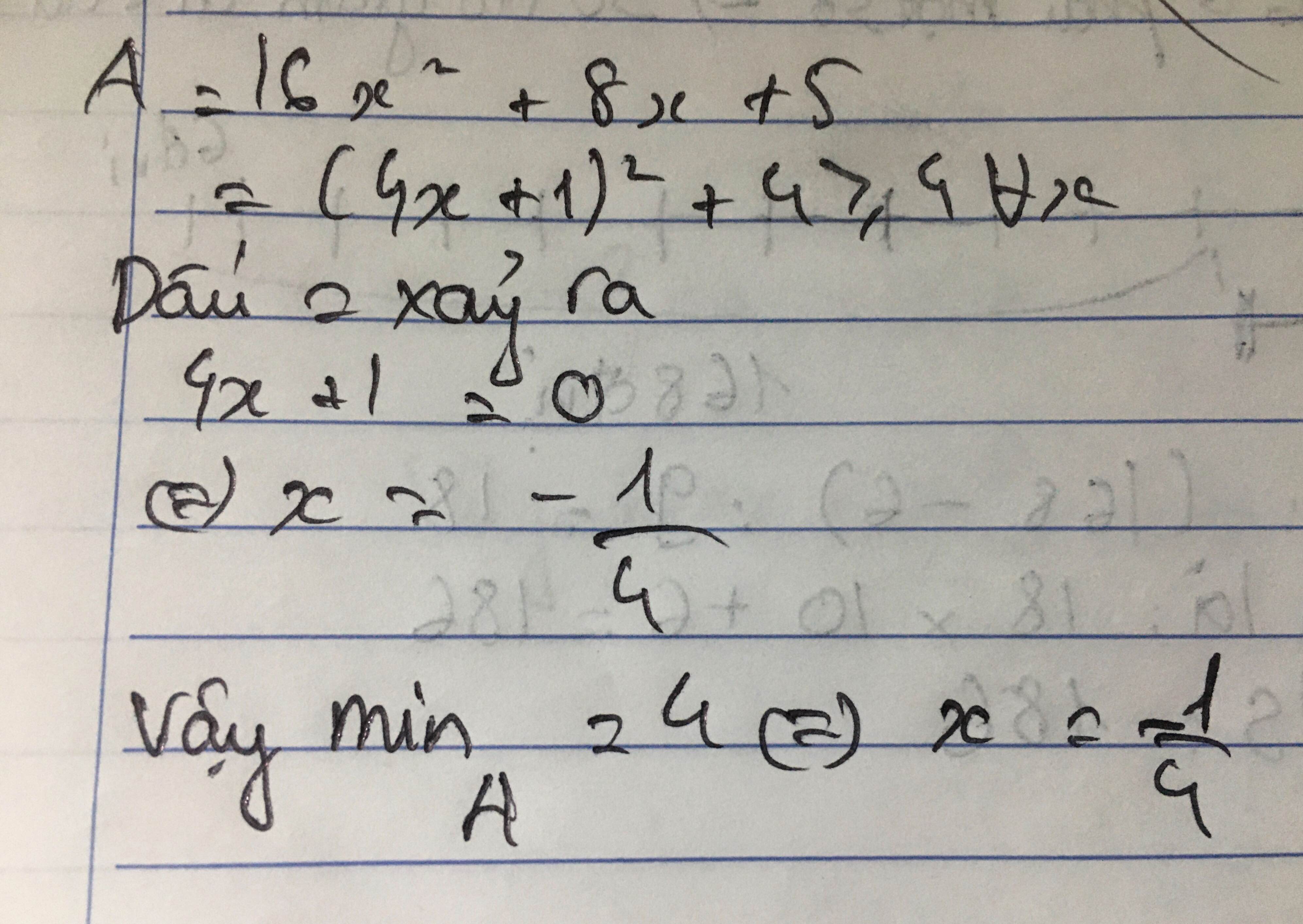
A = 16x2 - 8x + 5
A = [ ( 4x )2 - 2 . 4x . 1 + 1 ] + 4
A = ( 4x - 1 )2 + 4
Vì ( 4x - 1 )2 \(\ge\) 0 \(\forall\)x
=> ( 4x - 1 )2 + 4 \(\ge\)4 \(\forall\)x
=> A \(\ge\)4 \(\forall\)x
=> A = 4 <=> ( 4x - 1 )2 = 0
<=> 4x - 1 = 0
<=> 4x = 1
<=> x = \(\frac{1}{4}\)
Vậy A min = 4 <=> x = \(\frac{1}{4}\)