DN
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
. Giá trị a +b
CM
26 tháng 2 2017
Đáp án D
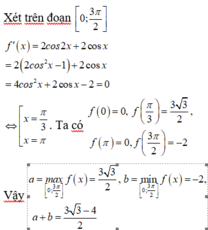
Chú ý: Có thể sử dụng chức năng TABLE của
MTCT để nhìn giá trị lớn nhất, giá trị nhỏ nhất
giúp bài toán làm nhanh hơn.
T
Tìm giá trị nhỏ nhất của P=2sinx+sin2x trên [0;3pi/2].
mọi người đừng dùng đạo hàm ạ em chưa được học
0
HP
15 tháng 8 2021
a, \(y=sin^2x-2sinx+3cos^2x\)
\(=sin^2x-2sinx+3\left(1-sin^2x\right)\)
\(=3-2sinx-2sin^2x\)
Đặt \(sinx=t\left(t\in\left[0;1\right]\right)\)
\(\Rightarrow y=f\left(t\right)=3-2t-2t^2\)
\(\Rightarrow y_{min}=min\left\{f\left(0\right);f\left(1\right)\right\}=-1\)
\(y_{max}=max\left\{f\left(0\right);f\left(1\right)\right\}=3\)
HP
15 tháng 8 2021
b, \(y=sinx-cosx+sin2x+5\)
\(=sinx-cosx-\left(sinx-cosx\right)^2+6\)
Đặt \(sinx-cosx=t\left(t\in\left[-\sqrt{2};\sqrt{2}\right]\right)\)
\(\Rightarrow y=f\left(t\right)=-t^2+t+6\)
\(\Rightarrow y_{min}=min\left\{f\left(-\sqrt{2}\right);f\left(0\right)\right\}=4-\sqrt{2}\)
\(y_{max}=max\left\{f\left(-\sqrt{2}\right);f\left(0\right)\right\}=6\)
TS
0
PT
1
CM
3 tháng 10 2017
Ta có: -1 ≤ sin x ≤ 1
⇒ -2 ≤ -2sin x ≤ 2
⇒ 1 ≤ 3 – 2sin x ≤ 5
hay 1 ≤ y ≤ 5.
Vậy hàm số đạt giá trị lớn nhất bằng 5.
HT
1
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 9 2021
Đặt \(sinx=t\in\left[-1;1\right]\)
\(y=f\left(t\right)=t^2+2t\)
Xét hàm \(y=f\left(t\right)=t^2+2t\) trên \(\left[-1;1\right]\)
\(-\dfrac{b}{2a}=-1\in\left[-1;1\right]\)
\(f\left(-1\right)=-1\) ; \(f\left(1\right)=3\)
\(\Rightarrow y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
MQ
0
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 12 2020
\(y=\sqrt{3}sin2x-cos2x=2\left(\dfrac{\sqrt{3}}{2}sin2x-\dfrac{1}{2}cos2x\right)=2sin\left(2x-\dfrac{\pi}{6}\right)\)
Do \(-1\le sin\left(2x-\dfrac{\pi}{6}\right)\le1\Rightarrow-2\le y\le2\)
\(y_{max}=2\) khi \(sin\left(2x-\dfrac{\pi}{6}\right)=1\)
\(y_{min}=-2\) khi \(sin\left(2x-\dfrac{\pi}{6}\right)=-1\)
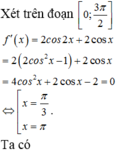
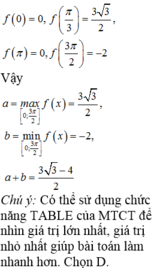
\(y=2sinx+sin2x\Rightarrow y'=2cosx+2cos2x=4cos^2x+2cosx-2\)
\(y'=0\Rightarrow\left[{}\begin{matrix}cosx=-1\\cosx=\frac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\pi+k2\pi\\x=\frac{\pi}{3}+k2\pi\\x=-\frac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(y\left(\pi\right)=0\) ; \(y\left(\frac{\pi}{3}\right)=\frac{3\sqrt{3}}{2}\); \(y\left(-\frac{\pi}{3}\right)=-\frac{3\sqrt{3}}{2}\)
\(\Rightarrow y_{max}=\frac{3\sqrt{3}}{2}\) khi \(x=\frac{\pi}{3}+k2\pi\)
Giải kiểu lớp dưới cũng được, hơi mất thời gian 1 chút thôi:
\(P=2sinx+2sinx.cosx=2sinx\left(cosx+1\right)\)
Áp dụng BĐT \(4ab\le\left(a+b\right)^2\) ta có:
\(P=\frac{1}{2\sqrt{3}}.4.\sqrt{3}sinx\left(cosx+1\right)\le\frac{1}{2\sqrt{3}}\left(\sqrt{3}sinx+cosx+1\right)^2\)
\(\Rightarrow P\le\frac{2}{\sqrt{3}}\left(\frac{\sqrt{3}}{2}sinx+\frac{1}{2}cosx+\frac{1}{2}\right)^2\)
\(\Rightarrow P\le\frac{2}{\sqrt{3}}\left[sin\left(x+\frac{\pi}{6}\right)+\frac{1}{2}\right]^2\le\frac{2}{\sqrt{3}}\left(1+\frac{1}{2}\right)^2=\frac{3\sqrt{3}}{2}\)
\(\Rightarrow P_{max}=\frac{3\sqrt{3}}{2}\)
Dấu "=" xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}sin\left(x+\frac{\pi}{6}\right)=1\\\sqrt{3}sinx=cosx+1\end{matrix}\right.\) \(\Rightarrow x=\frac{\pi}{3}+k2\pi\)
Mà tưởng lớp 11 học đạo hàm rồi chứ