Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giaỉ bất phương trình:
\(2x-1>1\\ < =>2x>1+1\\ =>2x>2\\ =>x>\dfrac{2}{2}\\ < =>x>1\)
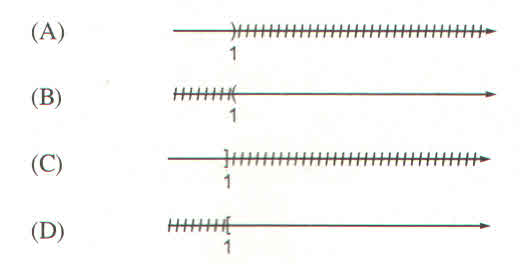
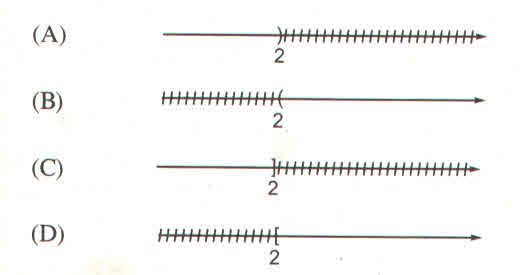
Vậy: tập nghiệm của bất phương trình là S= \(\left\{x|x>1\right\}\)
Biễu diễn tập nghiệm:
Chọn hình B.

a).
\(x^5+x+1=\left(x^5+x^4+x^3\right)-\left(x^4+x^3+x^2\right)+\left(x^2+x+1\right)\\ =\left(x^2+x+1\right)\left(x^3-x^2\right)\)
b).\(x^8+x^7+1=\left(x^8+x^7+x^6\right)-\left(x^6+x^5+x^4\right)+\left(x^5+x^4+x^3\right)-\left(x^3+x^2+x\right)+\left(x^2+x+1\right)\\ =\left(x^2+x+1\right)\left(x^6-x^4+x^3-x+1\right)\)
d).
\(x^7+x^5+1=\left(x^7+x^6+x^5\right)-\left(x^6+x^5+x^4\right)+\left(x^5+x^4+x^3\right)-\left(x^3+x^2+x\right)+\left(x^2+x+1\right)\\ =\left(x^2+x+1\right)\left(x^5-x^4+x^3-x+1\right)\)
e).
\(x^8+x^4+1=x^8+2x^4+1-x^4\\ =\left(x^4+1\right)^2-\left(x^2\right)^2\\ =\left(x^4+x^2+1\right)\left(x^4-x^2+1\right)\\ =\left(x^4-x^2+1\right)\left(x^2+x+1\right)\left(x^2-x+1\right)\)

Câu 1: 4cm
Câu 2: 6cm
Câu 3: 90o
Câu 4: -108
Câu 5: 2
Câu 6: 14
Câu 7: 43
Câu 8: -1
Câu 9: -3
Câu 10: -26
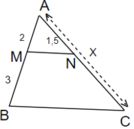



Ta có: MN//BC ⇒ AM/AB = AN/AC ⇔ 2/5 = 1,5/x ⇒ x = 5.1,5/2 = 3,75
Chọn đáp án C.