Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lỗi sai: Khi chuyển vế hạng từ -3 từ vế trái sang vế phải mà không đổi dấu.
Sửa lại:
2t – 3 + 5t = 4t + 12
⇔ 2t + 5t – 4t = 12 + 3
⇔ 3t = 15
⇔ t = 5.
Vậy phương trình có nghiệm duy nhất t = 5.

Sai ở phương trình thứ hai, chuyển vế hạng tử -3 từ vế trái sang vế phải mà không đổi dấu.
Giải lại: 2t - 3 + 5t = 4t + 12
<=> 2t + 5t - 4t = 12 + 3
<=> 3t = 15
<=> t = 5
Vậy phương trình có nghiệm duy nhất t = 5

Hướng dẫn giải:
a) 3x -11 = 0 <=> 3x = 11 <=> x = 113113
<=> x ≈ 3, 67
Nghiệm gần đúng là x = 3,67.
b) 12 + 7x = 0 <=> 7x = -12 <=> x = −127−127
<=> x ≈ -1,71
Nghiệm gần đúng là x = -1,71.
c) 10 - 4x = 2x - 3 <=> -4x - 2x = -3 - 10
<=> -6x = -13 <=> x = 136136 <=> x ≈ 2,17
Nghiệm gần đúng là x = 2, 17.
Hướng dẫn giải:
a) Sai ở phương trình thứ hai chuyển vế hạng tử -6 từ vế trái sang vế phải, hạng tử -x từ vế phải sang vế trái mà không đổi dấu.
Giải lại: 3x - 6 + x = 9 - x
<=> 3x + x + x = 9 + 6
<=> 5x = 15
<=> x = 3
Vậy phương trình có nghiệm duy nhất x = 3
b) Sai ở phương trình thứ hai, chuyển vế hạng tử -3 từ vế trái sang vế phải mà không đổi dấu.
Giải lại: 2t - 3 + 5t = 4t + 12
<=> 2t + 5t - 4t = 12 + 3
<=> 3t = 15
<=> t = 5
Vậy phương trình có nghiệm duy nhất t = 5

Lỗi sai: Khi chuyển vế hạng tử -x từ vế phải sang vế trái và hạng tử -6 từ vế trái sang vế phải không đổi dấu của hạng tử đó.
Sửa lại:
3x – 6 + x = 9 – x
⇔ 3x + x + x = 9 + 6
⇔ 5x = 15
⇔ x = 3.
Vậy phương trình có nghiệm duy nhất x = 3.

a) 5 - 4x = 3x - 9
\(\Leftrightarrow5-4x-3x+9=0\)
\(\Leftrightarrow14-7x=0\)
\(\Leftrightarrow7x=14\Leftrightarrow x=2\)
Vậy \(S=\left\{2\right\}\)
b) \(\left(x-4\right)\left(3x+9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\3x+9=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)
Vậy \(S=\left\{-3;4\right\}\)
c) \(\dfrac{x}{x+4}+\dfrac{12}{x-4}=\dfrac{4x+48}{x\cdot x-16}\)(1)
ĐKXĐ: \(x\ne\pm4\)
\(\left(1\right)\Leftrightarrow\dfrac{x\left(x-4\right)+12\left(x+4\right)-4x-48}{\left(x+4\right)\left(x-4\right)}=0\)
\(\Leftrightarrow x^2-4x+12x+48-4x-48=0\)
\(\Leftrightarrow x^2+4x=0\)
\(\Leftrightarrow x\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(TM\right)\\x=-4\left(KTM\right)\end{matrix}\right.\)
Vậy \(S=\left\{0\right\}\)
d) \(4-2x=7-x\)
\(\Leftrightarrow4-2x-7+x=0\)
\(\Leftrightarrow-x-3=0\)
\(\Leftrightarrow-x=3\Leftrightarrow x=-3\)
Vậy \(S=\left\{-3\right\}\)
e) \(\left(x+4\right) \left(8-4x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\8-4x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=2\end{matrix}\right.\)
Vậy \(S=\left\{-4;2\right\}\)
f) \(\dfrac{x}{x+5}+\dfrac{11}{x-5}=\dfrac{x+55}{x\cdot x-25}\left(2\right)\)
ĐKXĐ: \(x\ne\pm5\)
\(\left(2\right)\Leftrightarrow\dfrac{x\left(x-5\right)+11\left(x+5\right)-x-55}{\left(x+5\right)\left(x-5\right)}=0\)
\(\Leftrightarrow x^2-5x+11x+55-x-55=0\)
\(\Leftrightarrow x^2+5x=0\)
\(\Leftrightarrow x\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(TM\right)\\x=-5\left(KTM\right)\end{matrix}\right.\)
Vậy \(S=\left\{0\right\}\)
g) \(\dfrac{3x+2}{2}-\dfrac{3x+1}{6}=\dfrac{5}{3}+2x\)
\(\Leftrightarrow\dfrac{3\left(3x+2\right)-3x-1-10-12x}{6}=0\)
\(\Leftrightarrow9x+6-3x-1-10-12x=0\)
\(\Leftrightarrow-6x-5=0\)
\(\Leftrightarrow-6x=5\)
\(\Leftrightarrow x=-\dfrac{5}{6}\)
Vậy \(S=\left\{-\dfrac{5}{6}\right\}\)
h) \(2x-\left(3-5x\right)=4\left(x+3\right)\)
\(\Leftrightarrow2x-3+5x-4x-12=0\)
\(\Leftrightarrow3x-15=0\)
\(\Leftrightarrow x=5\)
Vậy \(S=\left\{5\right\}\)
i) \(3x-6+x=9-x\)
\(\Leftrightarrow3x-6+x-9+x=0\)
\(\Leftrightarrow5x-15=0\)
\(\Leftrightarrow x=3\)
Vậy \(S=\left\{3\right\}\)
k)\(2t-3+5t=4t+12\)
\(\Leftrightarrow2t-3+5t-4t-12=0\)
\(\Leftrightarrow3t-15=0\)
\(\Leftrightarrow t=5\)
Vậy \(S=\left\{5\right\}\)

x + 1 x 2 + 6 x + 9 = x 3 + 6 x 2 + 9 x + x 2 + 6 x + 9 = x 3 + 7 x 2 + 15 x + 9 x + 3 x 2 + 3 = x 3 + 3 x + 3 x 2 + 9
Ta có: x + 1 x 2 + 6 x + 9 ≠ x + 3 x 2 + 3
Vậy đẳng thức sai.
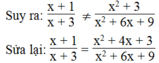

sai ở chỗ là chia cả hai vế cho x-1 nên đã làm mất nghiệm.
giải lại:
\(\left(x-1\right)=\left(x-1\right)\left(x-3\right)\)
\(\Leftrightarrow\left(x-1\right)-\left(x-1\right)\left(x-3\right)=0\).
\(\Leftrightarrow\left(x-1\right)\left(1-x+3\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(4-x\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=1\\x=4\end{cases}}\)
Bài đầy đủ đây đúng ko
a) 3x - 6 + x = 9 - x
<=> 3x + x - x = 9 - 6
<=> 3x = 3
<=> x =1
Sai ở chỗ phương trình thứ chuyển vế hạng tử -6 từ vế trái sang vế phải, hạng tử -x từ vế phải sang vế trái mà không đổi dấu
a) Giải lại:
<=> 3x + x + x = 9 + 6
<=> 5x = 15
<=> x = 3
b) Sai ở phương trình thứ 2, chuyển số hạng tử -3 từ vế trái sang vế phải mà ko đổi dấu
Giải lại:
<=> 2t + 5t - 4t = 12 + 3
<=> 3t = 15
<=> t = 5