K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
J
6
1 tháng 2 2019
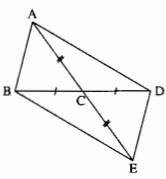
Giải
Ta có: ∆ACB = ∆ ECD(c.g.c)
∆ACD = ∆ECB(c.g.c)
∆ABD = ∆EDB(c.g.c)
∆ABE = ∆EDA(c.g.c)
1 tháng 2 2019
A B C D E
Ta có: ∆ACB = ∆ ECD(c.g.c)
∆ACD = ∆ECB(c.g.c)
∆ABD = ∆EDB(c.g.c)
∆ABE = ∆EDA(c.g.c)
NP
3
R
12 tháng 5 2018
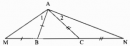
Ta có:
AB=AC(gt)(1);AM=12AB(gt)(2);AN=12AC(gt)(3)AB=AC(gt)(1);AM=12AB(gt)(2);AN=12AC(gt)(3)
Từ (1), (2) và (3) suy ra: AM = AN
Xét hai tam giác vuông AMI và ANI, ta có:
ˆAMI=ˆANI=90∘AMI^=ANI^=90∘
AM = AN (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆AMI = ∆ANI (cạnh huyền, cạnh góc vuông)
Suy ra ˆA1=ˆA2A1^=A2^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆBAC
Y
0
A
27 tháng 6 2019
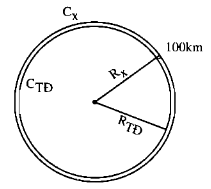
a) Vì vệ tinh cách mặt đất là 100km nên chu vi vệ tinh quay vòng hơn chu vi trái đất một khoảng 2.3,14.100 nên nhỏ hơn 1000km
b) Gọi bán kính của Trái Đất \(R_{TD}\), bán kính quỹ đạo vệ tinh \(R_{VT}\)
Chu vi trái đất \(2\pi R_{TD}\), chu vi quỹ đạo vệ tinh \(2\pi R_{VT}\)
Vì chu vi của đường tròn tỉ lệ thuận với bán kính nên ta có:
\(\frac{2\pi R_{VT}}{2\pi R_{TD}}=\frac{R_{VT}}{R_{TD}}\)
\(\Rightarrow\frac{2\pi R_{VT}-2\pi R_{TD}}{2\pi R_{TD}}=\frac{R_{VT}-R_{TD}}{R_{TD}}\)
\(\Rightarrow2\pi R_{VT}-2\pi R_{TD}=\frac{2\pi R_{TD}\left(R_{VT}-R_{TD}\right)}{R_{TD}}\)
\(\Rightarrow2\pi R_{VT}-2\pi R_{TD}=2\pi.100\approx628\left(km\right)\)
Quãng đường vệ tinh bay dài hơn chu vi trái đất khoảng 628km.
Hình nào bạn