
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Phương pháp:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Cách giải:
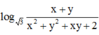
![]()
<=> ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (2)
(2)
Đặt ![]()
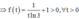
=> f(t) đồng biến trên (0;+∞)
![]()
![]()
<=> ![]()
<=> ![]()
![]()
Khi đó, 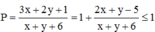
vì 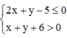
Vậy Pmax = 1 khi và chỉ khi 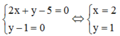

Đáp án C
Phương pháp giải:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Lời giải:
log 3 x + y x 2 + y 2 + x y + 2 = x ( x - 3 ) + y ( y - 3 ) + x y (1)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (2)
(2)
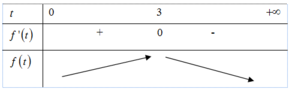
Đặt ![]()
![]()
=> f(t) đồng biến trên (0;+∞)
![]()
![]()
![]()
![]()
![]()
Khi đó, 
vì 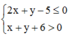
Vậy Pmax = 1 khi và chỉ khi 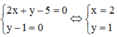

Vì \(\left(2x+1\right)\left(y-3\right)=12\)
\(\Rightarrow2x+1;y-3\inƯ\left(12\right)=\left\{-12;-6;-4;-3;-2;-1;1;2;3;4;6;12\right\}\)
Vì \(2x+1\) là số lẻ nên \(2x+1\in\left\{-3;-1;1;3\right\}\)
Ta có bảng sau:
| 2x+1 | -3 | -1 | 1 | 3 |
| 2x | -4 | -2 | 0 | 2 |
| x | -2 | -1 | 0 | 1 |
| y-3 | -4 | -12 | 12 | 4 |
| y | -1 | -9 | 15 | 7 |
Vậy \(\left(x;y\right)\in\left\{\left(-2;-1\right);\left(-1;-9\right);\left(0;15\right);\left(1;7\right)\right\}\)
Ta có:
\(xy+3x-7y=21\)
\(\Rightarrow x.\left(y+3\right)-7y-21=21-21=0\)
\(x\left(y+3\right)-\left(21+7y\right)=0\)
\(x.\left(y+3\right)-7.\left(y+3\right)=0\)
\(\left(x-7\right)\left(y+3\right)=0\)
\(\Rightarrow x-7=0\) hoặc \(y+3=0\)
TH1: x-7=0
x=0+7=7
TH2:y+3=0
y=0-3=-3
Vậy x=7; y=-3

Đáp án C.
Ta có x x − 3 + y y − 3 + x y
= x 2 + y 2 + x y − 3 x − 3 y = x 2 + y 2 + x y + 2 − 3 x + y − 2
Khi đó, giả thiết trở thành:
log 3 x + y x 2 + y 2 + x y + 2 = x 2 + y 2 + x y + 2 − 3 x + y − 2
⇔ log 3 x + y − log 3 x 2 + y 2 + x y + 2 = x 2 + y 2 + x y + 2 − 3 x + y − 2
⇔ 3 x + y + log 3 3 x + y = x 2 + y 2 + x y + 2 + log 3 x 2 + y 2 + x y + 2
Xét hàm số f t = t + log 3 t trên khoảng 0 ; + ∞ ,
có f ' t = 1 + 1 t ln 3 > ; ∀ t > 0.
Suy ra f( t) là hàm số đồng biến trên 0 ; + ∞
mà f 3 x + y = f x 2 + y 2 + x y + 2
⇔ 2 x + y 2 − 6 2 x + y + 5 = − 3 y − 1 2 ≤ 0 ⇔ 1 ≤ 2 x + y ≤ 5.
Khi đó P = 1 + 2 x + y − 5 x + y + 6 ≤ 1
vì 2 x + y − 5 ≤ 0 x + y + 6 > 0 . Vậy P m a x = 1.

Chọn A.
Phương pháp:
- Biến đổi điều kiện bài cho về dạng f u = f v với u, v là các biểu thức của x, y.
- Xét hàm f t suy ra mối quan hệ của u, v rồi suy ra x, y.
- Đánh giá P theo biến t=x+y bằng cách sử dụng phương pháp hàm số.
Cách giải:
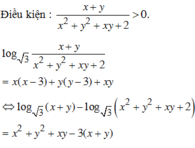
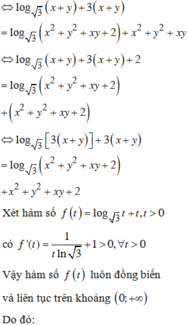
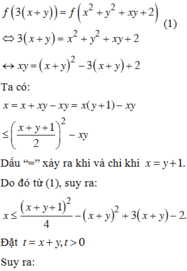
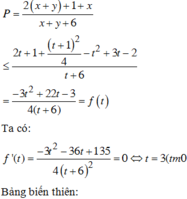



bạn ơi, xem lại đề ra 1 chút, hình như có câu sai đề thì phải
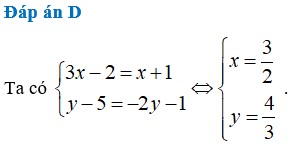
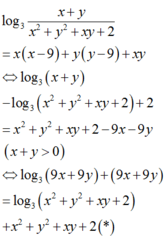

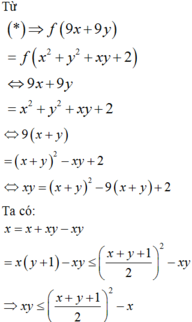
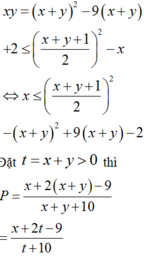
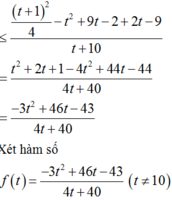
Viết sai ùi kìa là 17-xy
3x-2y=27-xy
3x-2y+xy=27
3x+xy-2y=27
x(3+y)-2y-6=27-6
x(3+y)-(2y+6)=21
x(3+y)-2(y+3)=21
(y+3)(x-2)=21
Ta có bảng giá trị: