Tìm các số nguyên a sao cho 3a

NM

Nguyễn Minh Vũ

3 tháng 1 2018 - olm

cho phép toán * thỏa mãn: với hai số tự nhiên a và b có: a*b=3a+b^a. Tìm các số nguyên tố x,y sao cho 2*x+y*4-8 cũng là số nguyên tố

#Hỏi cộng đồng OLM #Toán lớp 6

4

NB

Nguyễn Bảo Long

3 tháng 1 2018

Ek bạn , bạn có chơi nr ko

Đúng(0)

NM

Nguyễn Minh Vũ

3 tháng 1 2018

kb nha minh t i c k nha

Đúng(0)

PT

Pham Trong Bach

9 tháng 12 2019

Tìm các số nguyên a sao cho

a) 2 a ⋮ a − 1

b) 3 a − 8 ⋮ a − 4

c) a 2 + 7 là bội của a+1

#Hỏi cộng đồng OLM #Toán lớp 6

3

CM

Cao Minh Tâm

9 tháng 12 2019

Đúng(0)

NM

Ngô Mạnh Hiếu

21 tháng 2 2021

Tìm số nguyên a để phân số sau cũng là số nguyên: 6a - 18 a - 5 Đáp số a ∈ { }

Đúng(0)

LT

Lê Thị Mai Phương

4 tháng 3 2020 - olm

Tìm các số nguyên a sao cho
a) a + 5 chia hết a – 1
b) 2a chia hết a – 1
c) 3a – 8 chia hết a – 4
d) a^2 + a + 1 chia hết a + 1

#Hỏi cộng đồng OLM #Toán lớp 6

2

CX

cường xo

5 tháng 3 2020

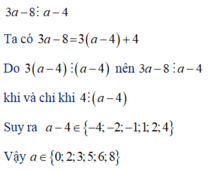
làm câu d) thui thấy tụi quá

ta có : a² + a + 1 \(⋮\)a + 1

=) [ a² + a + 1 - ( a + 1 ) \(⋮\)a + 1

=) a² \(⋮\)a + 1

=) [ a² - ( a + 1 )] \(⋮\) a + 1

=) [ a² - a( a + 1 )] \(⋮\)a + 1

=) a \(⋮\)a + 1

=) a \(\in\){ 0 : -2 }

Đúng(0)

NF

Napkin ( Fire Smoke Team )

5 tháng 3 2020

\(a,a+5⋮a-1\)

\(=>a-1+6⋮a-1\)

Do \(a-1⋮a-1\)

\(=>6⋮a-1\)

\(=>a-1\inƯ\left(6\right)=\left\{-6;-3;-2;-1;1;2;3;6\right\}\)

\(=>a\in\left\{-5;-2;-1;0;2;3;4;7\right\}\)

\(b,2a⋮a-1\)

\(=>2a-2+2⋮a-1\)

\(=>2.\left(a-1\right)+2⋮a-1\)

\(Do:2.\left(a-1\right)⋮a-1\)

\(=>2⋮a-1\)

\(=>a-1\inƯ\left(-2;-1;1;2\right)\)

\(=>a\in\left\{-1;0;2;3\right\}\)

\(c,3a-8⋮a-4\)

\(=>3.\left(a-4\right)+4⋮a-4\)

\(Do:3.\left(a-4\right)⋮a-4\)

\(=>4⋮a-4\)

\(=>a-4\inƯ\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\)

\(=>a\in\left\{0;2;3;5;6;8\right\}\)

D thì bạn kia làm rồi

Đúng(0)

TQ

trần quang minh

7 tháng 2 2020 - olm

tìm số nguyên a sao cho:

3a-8 chia hết cho a-4

giúp mình giải với

#Hỏi cộng đồng OLM #Toán lớp 6

4

M

๛๖ۣۜMĭη²ƙ⁸࿐

7 tháng 2 2020

3a-8 chia hết cho a-4

Ta có : a-4 chia hết cho a-4

=> 3(a-4) chia hết cho a-4

<=>3a-12 chia hết cho a-4

Mà 3a-8 chia hết cho a-4

=>[(3a-12)-(3a-8)] chia hết cho a-4

<=> -4 chia hết cho a-4

=> a-4 thuộc U(-4)={1;-1;2;-2;4;-4}

Ta có bảng tương ứng :

( bạn tự lập bảng nha )

HỌC TỐT !

Đúng(0)

S

sjfdksfdkjlsjlfkdjdkfsl

7 tháng 2 2020

3a-8 \(⋮\)a-4 khi \(A=\frac{3a-8}{a-4}\)là số nguyên (a-4 khác 0 => a khác 4)

\(A=\frac{3a-8}{a-4}=\frac{3a-12+4}{a-4}=3+\frac{4}{a-4}\)

Để A là số nguyên thì \(\frac{4}{a-4}\)cũng phải là số nguyên

=> \(4⋮a-4\)

=> \(\left(a-4\right)\in\)tập (cộng trừ 1, cộng trừ 2, cộng trừ 4)

(kẻ bảng) => a = 5; 3; 6; 2; 8; 0

Đúng(0)

TT

Trần Thị Hạnh

22 tháng 2 2020 - olm

Tìm các số nguyên a sao cho

a)a+5chia hết cho a-1

b)2a chia hết cho a-1

c)3a-8 chia hết cho a-4

d)a mũ 2 +a+1 chia hết cho a+1

Làm nhanh và đầy đủ lời giải giúp mình nha🥰🥰

Tks

#Hỏi cộng đồng OLM #Toán lớp 6

1

2U

๖²⁴ʱんuﾘｲú❄✎﹏

22 tháng 2 2020

\(a,a+5⋮a-1\)

\(a-1+6⋮a-1\)

Vì \(a-1⋮a-1\)

\(6⋮a-1\)

\(\Rightarrow a-1\inƯ\left(6\right)=\left\{\pm1;\pm2;\pm3;\pm6\right\}\)

Tự lập bảng ...

\(b,2a⋮a-1\)

\(2a-2+2⋮a-1\)

\(2\left(a-1\right)+2⋮a-1\)

Vì \(2\left(a-1\right)⋮a-1\)

\(2⋮a-1\)

\(\Rightarrow a-1\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)

Tự lập bảng ...

\(c,3a-8⋮a-4\)

tương tự phần b

Đúng(0)

KH

kiss Hoàng Tử Kai ss

13 tháng 2 2016 - olm

1/ Tìm số nguyên n sao cho n + 2 chia hết cho n -3

2/ Tìm tất cả các số nguyên a biết: (6a +1) chia hết cho ( 3a -1)

3/ tìm 2 số nguyên a , b biết :a > 0 và a. (b - 2) =3

#Hỏi cộng đồng OLM #Toán lớp 6

1

TA

Tuấn Anh Phan Nguyễn

13 tháng 2 2016

3/ => a(b-2) thuộc Ư(3) = {1;3;-1;-3}

Mà a > 0

=> a thuộc {1;3}

Ta có bảng kết quả:

a	1	3
b-2	3	1
b	5	3

Đúng(0)

DC

Đặng Công Tùng

22 tháng 1 2018 - olm

Tìm tất cả các số nguyên a biết :a^2 +3a + 4 chia hết cho a-1

#Hỏi cộng đồng OLM #Toán lớp 6

1

TQ

Trịnh Quỳnh Nhi

22 tháng 1 2018

Ta có a²+3a+4 chia hết cho a-1

=> a²-a+4a-4+8 chia hết cho a-1

=> a(a-1)+4(a-1)+8 chia hết cho a-1

=> (a-1)(a+4)+8 chia hết cho a-1

Mà (a-1)(a+4) chia hết cho a-1 nên 8 chia hết cho a-1 và a là số nguyên

=> a-1 thuộc {-8;-4;-2;-1;1;2;4;8}

=> a thuộc { -7;-3;-1;0;2;3;5;9}

Đúng(0)

➶➶➶➶ 𝕷𝖚𝖋𝖋𝖞 ➷➷➷➷

26 tháng 2 2021

Bài 1:Tìm số nguyên tố p, sao cho p+2 và p+4 cũng là các số nguyên tố.Bài 2. Cho p và 2p + 1 là các số nguyên tố ( p > 3). Hỏi 4p + 1 là số nguyên tố hay hợp số?Bài 3:a) Tìm số nguyên tố p,sao cho p + 4 và p + 8 cũng là các số nguyên tố.b) Tìm số nguyên tố p, sao cho p + 6, p + 8, p + 12, p + 14 cũng là các số nguyên tố.Bài 4: Tìm số tự nhiên nhỏ nhất có 12 ước số.Bài 5: Chứng minh rằng với mọi số...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 6

5

👁💧👄💧👁

26 tháng 2 2021

Bài 1:

Nếu p = 2 thì p + 2 = 2 + 2 = 4 không là số nguyên tố

2 + 4 = 6 không là số nguyên tố

Vậy p = 2 không thỏa mãn

Nếu p = 3 thì p + 2 = 3 + 2 = 5 là số nguyên tố

3 + 4 = 7 là số nguyên tố

Vậy p = 3 thỏa mãn

Nếu p > 3 thì p = 3k + 1 hoặc p = 3k + 2

Khi p = 3k + 1 thì p + 2 = 3k + 1 + 2 = 3k + 3 = 3(k + 1) không là số nguyên tố

Vậy p = 3k + 1 không thỏa mãn

Khi p = 3k + 2 thì p + 4 = 3k + 2 + 4 = 3k + 6 = 3(k + 2) không là số nguyên tố

Vậy p = 3k + 2 không thỏa mãn

Vậy p = 3 thỏa mãn duy nhất.

Đúng(3)

👁💧👄💧👁

26 tháng 2 2021

Bài 2:

Khi ta xét 3 số tự nhiên liên tiếp 4p; 4p + 1; 4p + 2 thì chắc chắn sẽ có một số chia hết cho 3

p là số nguyên tố; p > 3 nên p không chia hết cho 3 => 4p không chia hết cho 3

Ta thấy 2p + 1 là số nguyên tố; p > 3 => 2p + 1 > 3 nên 2p + 1 không chia hết cho 3 => 2(2p + 1) không chia hết cho 3 -> 4p + 2 không chia hết cho 3

Vì thế 4p + 1 phải chia hết cho 3

Mà p > 3 nên 4p + 1 > 3

=> 4p + 1 không là số nguyên tố. 4p + 1 là hợp số.

Đúng(2)

NT

Nguyễn Thị Vân Anh

24 tháng 3 2020 - olm

Dạng 6: Bội và ước của số nguyên B

Bài 1: Tìm các số nguyên a sao cho:

a) a + 5 ⋮ a - 2 b) 3a ⋮ a - 1

c) 5a - 8 ⋮ a - 4 d) a2 + a + 2 ⋮ a + 1

Bài 2: Tìm số nguyên n sao cho:

a) 4n - 3 ⋮ n b) -13 là bội của 2n - 1

#Hỏi cộng đồng OLM #Toán lớp 6

1

TL

Tran Le Khanh Linh

24 tháng 3 2020

Bài 1

a) Ta có: a+5=a-2+7

=> 7 chia hết cho a-2 hay a-2 thuộc Ư (7)={-7;-1;1;7}
=> a={-5;1;3;9}

b) 3a=3(a-1)+3

=> 3 chia hết cho a-1 hay a-1 thuộc Ư (3)={-3;-1;1;3}

=> a={-2;0;2;4}

c) Ta có 5a-8=5(a-4)+12

=> 12 chia hết cho a-4

hay a-4 thuộc Ư (12)={-12;-6;-4;-3;-2;-1;1;2;3;4;6;12}

=> a={-8;-2;0;1;2;3;5;6;7;8;10;16}

Bài 2:

a) 4n-3 chia hết cho n

=> 3 chia hết cho n hay n thuộc Ư (3)={-3;-1;1;3}

b) -13 là bội của 2n-1

=> 2n-1 thuộc Ư (-13)={-13;-1;1;13}

=> 2n={-12;0;2;14}

=> n={-6;0;1;7}

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP