
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a, b là số tự nhiên, với \(0\le a,b\le9\),\(a,b\in N\)
số đó ko chia hết cho 2 nhưng chia hết cho 5 => b = 5
số đó chia hết cho 9 thì tổng các chữ số phải chia hết cho 9
ta có 8 + 2 + 5 + a + 2 + 5 = 22 + a chia hết cho 9 <=> 22 + a \(\inƯ\left(9\right)\)
\(0\le a\le9\)<=>\(22\le22+a\le22+9\)<=>\(22\le22+a\le31\)
Mà 22 + a \(\in N\)
Vậy 22 + a = 27 (27 thỏa các điều kiện đã nêu)
=> a = 5

Để 825a2b chia hết cho 5 thì b có thể là 0 hoặc 5.
Mà 825a2b không chia hết cho 2 nên b=5.
Ta có: 825a25
Để 825a25 chia hết cho 9
thì 8+2+5+a+2+5 chia hết cho 9
hay 22+a chia hết cho 9
=> a=5
Vậy a=5 ; b=5

b: Đặt \(A=\overline{5a43b}\)
A chia hết cho 2 và 5 nên A có tận cùng là 0
=>b=0
=>\(A=\overline{5a430}\)
A chia hết cho 9
=>5+a+4+3+0 chia hết cho 9
=>a+12 chia hết cho 9
=>a=6
=>Số cần tìm là 56430
c: Đặt \(B=\overline{735a2b}\)
B chia hết cho 5 và không chia hết cho 2 nên b=5
=>\(B=\overline{735a25}\)
B chia hết cho 9
=>7+3+5+a+2+5 chia hết cho 9
=>a+22 chia hết cho 9
=>a=5
Vậy: Số cần tìm là 735525
d: Đặt \(C=\overline{5a27b}\)
C chia hết cho 2 và 5 nên C có tận cùng là 0
=>b=0
=>\(C=\overline{5a270}\)
C chia hết cho 9
=>5+a+2+7+0 chia hết cho 9
=>a+14 chia hết cho 9
=>a=4
Vậy: Số cần tìm là 54270
e: Đặt \(D=\overline{7a142b}\)
Vì D chia hết cho cả 2 và 5 nên D có tận cùng là 0
=>b=0
=>\(D=\overline{7a1420}\)
D chia hết cho 9
=>7+a+1+4+2+0 chia hết cho 9
=>a+14 chia hết cho 9
=>a=4
=>Số cần tìm là 741420
g: \(X=\overline{40ab}\)
X chia hết cho 2 và 5 nên b=0
=>\(X=\overline{40a0}\)
X chia hết cho 3
=>4+a+0+0 chia hết cho 3
=>a+4 chia hết cho 3
=>\(a\in\left\{2;5;8\right\}\)
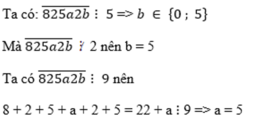
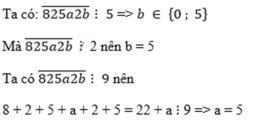
Chia hết cho 5 mà không chia hết cho 2 => b=5
Ta có, tổng các chữ số của số trên là: 8 + 2 + 5 + a + 2 + b = 8 + 2 + 5 + a + 2 + 5 = 22 + a
Để số trên chia hết cho 9 thì (22+a) chia hết cho 9, vậy a = 5 (Để: 22+a=27, và 27:9=3)
Vậy: Với a=5;b=5 thì số 825a2b chia hết cho cả 5 và 9 nhưng không chia hết cho 2