Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo bài ra ta có :
x,y,z tỉ lệ nghịch với 2;3;4 và a + b + c = 300
\(\Leftrightarrow2x=3y=4z\)
\(\Leftrightarrow\frac{2x}{12}=\frac{3y}{12}=\frac{4z}{12}\)
\(\Rightarrow\frac{x}{6}=\frac{y}{4}=\frac{z}{3}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{6}=\frac{y}{4}=\frac{z}{3}=\frac{x+y+z}{6+4+3}=\frac{300}{13}\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{6}=\frac{300}{13}\Rightarrow x=\frac{1800}{13}\\\frac{y}{4}=\frac{300}{13}\Rightarrow y=\frac{1200}{13}\\\frac{z}{3}=\frac{300}{13}\Rightarrow z=\frac{900}{13}\end{cases}}\)
Vậy ...

Ba số x,y,z tỉ lệ thuận với 3;5;7 nên theo tính chất về tỉ lệ thuận ta có:
x
3
=
y
5
=
z
7
Theo bài ra ta có z - y = 10
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
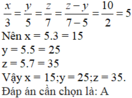

a) Ta có : 7x = 5z => x/5 = z/7 => x/15 = z/21 (1)
x/3 = y/2 => x/15 = y/10 (2)
Từ (1) và (2) suy ra \(\frac{x}{15}=\frac{y}{10}=\frac{z}{21}\)
Áp dụng t/c của dãy tỉ số bằng nhau
Ta có : \(\frac{x}{15}=\frac{y}{10}=\frac{z}{21}\)=> \(\frac{4x}{60}=\frac{3y}{30}=\frac{2z}{42}=\frac{4x-3y-2z}{60-30-42}=\frac{-2}{-12}=\frac{1}{6}\)
=> \(\hept{\begin{cases}\frac{x}{15}=\frac{1}{6}\\\frac{y}{10}=\frac{1}{6}\\\frac{z}{21}=\frac{1}{6}\end{cases}}\) => \(\hept{\begin{cases}x=\frac{1}{6}.15=\frac{15}{6}\\y=\frac{1}{6}.10=\frac{5}{3}\\z=\frac{1}{6}.21=\frac{7}{2}\end{cases}}\)
Vậy ...

a)Vì x;y;z tỉ lệ thuận với 2;3;5 nên x:y:z=2:3:5
x:|===|===|
y:|===|===|===|
z:|===|===|===|===|===|
62;93;155

2.Gọi hai số dương lần lượt là x và y
Theo đề bài ta có : \(\frac{x+y}{\frac{1}{35}}=\frac{x-y}{\frac{1}{210}}=\frac{xy}{\frac{1}{12}}\)
hay \(35\left(x+y\right)=210\left(x-y\right)=12\left(x\cdot y\right)\)
Mà \(BCNN\left(35,210,12\right)=420\)
=> \(\frac{35\left(x+y\right)}{420}=\frac{210\left(x-y\right)}{420}=\frac{12\left(x\cdot y\right)}{420}\)
=> \(\frac{x+y}{12}=\frac{x-y}{2}=\frac{x\cdot y}{35}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
+)\(\frac{x+y}{12}=\frac{x-y}{2}=\frac{\left(x+y\right)-\left(x-y\right)}{12-2}=\frac{2y}{10}=\frac{y}{5}\)(1)
+) \(\frac{x+y}{12}=\frac{x-y}{2}=\frac{\left(x+y\right)+\left(x-y\right)}{12+2}=\frac{2x}{14}=\frac{x}{7}\)(2)
=> Từ (1) và (2) => \(\frac{x}{7}=\frac{y}{5}\)
Đặt \(\frac{x}{7}=\frac{y}{5}=k\Rightarrow\orbr{\begin{cases}x=7k\\y=5k\end{cases}}\)
=> \(xy=7k\cdot5k=35k^2\)
=> \(35k^2=35\)
=> \(k^2=1\)
=> k = 1(loại âm vì đề bài cho 2 số dương)
Do đó : \(\frac{x}{7}=1\Rightarrow x=7\)
\(\frac{y}{5}=1\)=> \(y=5\)
Vậy x = 7,y = 5
1. Câu hỏi của I will shine on the sky - Toán lớp 7 - Học toán với OnlineMath

Gọi các phân số phải tìm theo theo thứ tự là a,b,c.Ta có:a+b+c= -187/60
ta có: a:b:c=2/5:3/4:5/6=0,4:0,75:0,(83)=40:75:83
dc:a/40=b/75=c/83--->a+b+c/40+75+83= -187/60:45= -17/1080
Từ đó : *a= -17/27
*b= -85/72
*c= -1411/1080
ĐÚNG 100% VÌ LÀM ĐI LÀM LẠI LẦN THỨ 3 MỚI RA
Bùi Anh Tuấn không đúng 100% đâu. -187/60:198 chứ không phải -187/60:45

Gọi 3 số đó lần lượt là: a, b, c
Ta có:
\(\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{4}}=\frac{c}{\frac{1}{5}}\) và a + b + c = 611
Áp dụng tính chất dãy tỉ số bằng nhau có:
\(\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{4}}=\frac{c}{\frac{1}{5}}=\frac{a+b+c}{\frac{1}{3}+\frac{1}{4}+\frac{1}{5}}=\frac{611}{\frac{47}{60}}=780\)
Suy ra: \(\frac{a}{\frac{1}{3}}=780\Rightarrow a=780\cdot\frac{1}{3}=260\)
\(\frac{b}{\frac{1}{4}}=780\Rightarrow b=780\cdot\frac{1}{4}=195\)
\(\frac{c}{\frac{1}{5}}=780\Rightarrow c=780\cdot\frac{1}{5}=156\)
Vậy 3 số đó lần lượt là: 260; 15; 156
Giải:
Ta có: \(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}\) và \(x+y+z=180\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}=\frac{x+y+z}{2+3+5}=\frac{180}{10}=18\)
+) \(\frac{x}{2}=18\Rightarrow x=36\)
+) \(\frac{y}{3}=18\Rightarrow y=54\)
+) \(\frac{z}{5}=18\Rightarrow z=90\)
Vậy bộ số \(\left(x,y,z\right)\) là \(\left(36,54,90\right)\)
Từ x,y,z tỉ lệ với 2,3,5 => \(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}\)
Áp dụng t/c dãy tỉ số bằng nhau, ta có:
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}=\frac{x+y+z}{2+3+5}=\frac{180}{10}=18\)
=> \(\begin{cases}x=36\\y=54\\z=90\end{cases}\)