S
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HT
0
HT
2
19 tháng 12 2016
Giải:
Ta có: \(3\left(a+1\right)=8\left(b+2\right)=12\left(c+3\right)\)
\(\Rightarrow\frac{3\left(a+1\right)}{24}=\frac{8\left(b+2\right)}{24}=\frac{12\left(c+3\right)}{24}\)
\(\Rightarrow\frac{a+1}{8}=\frac{b+2}{3}=\frac{c+3}{2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a+1}{8}=\frac{b+2}{3}=\frac{c+3}{2}=\frac{a+1+b+2+c+3}{8+3+2}=\frac{\left(a+b+c\right)+\left(1+2+3\right)}{13}=\frac{23+6}{13}=2\)
+) \(\frac{a+1}{8}=2\Rightarrow a=15\)
+) \(\frac{b+2}{3}=2\Rightarrow b=4\)
+) \(\frac{c+3}{2}=2\Rightarrow c=1\)
Vậy bộ số \(\left(a;b;c\right)\) là \(\left(15;4;1\right)\)
TQ
19 tháng 12 2016
Theo đề ta có:
3.(a+1) = 8.(b+2) = 12.(c+3) => \(\frac{3.\left(a+1\right)}{24}=\frac{8.\left(b+2\right)}{24}=\frac{12.\left(c+3\right)}{24}\)
=> \(\frac{a+1}{8}=\frac{b+2}{3}=\frac{c+3}{2}\)
Theo tính chất của dãy tỉ số bằng nhau. Ta có:
\(\frac{a+1}{8}=\frac{b+2}{3}=\frac{c+3}{2}\)\(=\frac{a+1+b+2+c+3}{8+3+2}=\frac{a+b+c+1+2+3}{13}=\frac{20+6}{13}=\frac{26}{13}=2\)
=> \(\frac{a+1}{8}=2\) => \(a+1=16\) => \(a=15\)
=> \(\frac{b+2}{3}=2\) => \(b+2=6\) => \(b=4\)
=> \(\frac{c+3}{2}=2\) => \(c+3=4\) => \(c=1\)
Vậy \(a=15\)
\(b=4\)
\(c=1\)
1 tháng 12 2021
\(1,4a=5b\Leftrightarrow\dfrac{a}{5}=\dfrac{b}{4}=\dfrac{b-a}{4-5}=\dfrac{27}{-1}=-27\\ \Leftrightarrow\left\{{}\begin{matrix}a=-135\\b=-108\end{matrix}\right.\\ 2,\dfrac{1}{3}x=\dfrac{1}{2}y=\dfrac{1}{5}z\Leftrightarrow\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{z}{5}=\dfrac{x+2y-z}{3+4-5}=\dfrac{8}{2}=4\\ \Leftrightarrow\left\{{}\begin{matrix}x=12\\y=8\\z=20\end{matrix}\right.\\ 3,\dfrac{1}{3}a=\dfrac{1}{2}b;\dfrac{1}{5}a=\dfrac{1}{7}c\\ \Leftrightarrow\dfrac{a}{15}=\dfrac{b}{10}=\dfrac{c}{21}=\dfrac{a+b+c}{15+10+21}=\dfrac{184}{46}=4\\ \Leftrightarrow\left\{{}\begin{matrix}a=60\\b=40\\c=84\end{matrix}\right.\)
30 tháng 12 2021
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{15}=\dfrac{b}{10}=\dfrac{c}{8}=\dfrac{a+b+c}{15+10+8}=\dfrac{11}{33}=\dfrac{1}{3}\)
Do đó: a=5; b=10/3; c=8/3
CN
0
NT
tìm 3 số a, b, c biết a -b +c =34 , a và b tỉ lệ thuận với 3 và 5 , b và c tỉ lệ nghịch với 5 và 4 .
0
HY
4
18 tháng 10 2016
Giải :
Theo đề bài ta có :
a và b tỉ lệ thuận với 3 và 5 : \(\frac{a}{3}=\frac{b}{5}\)(1)
b và c tỉ lệ ngịch với 5 và 4 : \(\frac{b}{\frac{1}{5}}=\frac{c}{\frac{1}{4}}\)(2)
=> \(\frac{b}{5}=\frac{c}{\frac{25}{4}}\)
Từ ( 1 ) và ( 2 ) => \(\frac{a}{3}=\frac{b}{5}=\frac{c}{\frac{25}{4}}\)
Theo t/c của dãy tỉ số bằng nhau ta có :
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{\frac{25}{4}}=\frac{a-b+c}{3-5+\frac{25}{4}}=\frac{34}{\frac{17}{4}}=8\)
\(\frac{a}{3}=8\Rightarrow a=8.3=24\)
\(\frac{b}{5}=8\Rightarrow b=8.5=40\)
\(\frac{c}{\frac{25}{4}}8\Rightarrow c=8.\frac{25}{4}=50\)
AT
18 tháng 10 2016
Theo bài ta có:
a và b tỉ lệ thuận với 3 và 5 : \(\frac{a}{3}\) = \(\frac{b}{5}\) (1)
b và c tỉ lệ nghịch với 5 và 4 : \(\frac{b}{\frac{1}{5}}\) = \(\frac{c}{\frac{1}{4}}\) (2)
\(\Rightarrow\) \(\frac{b}{5}\) = \(\frac{c}{\frac{25}{4}}\)
Từ (1) và (2) \(\Rightarrow\) \(\frac{a}{3}\) = \(\frac{b}{5}\) = \(\frac{c}{\frac{25}{4}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}\) = \(\frac{b}{5}\) = \(\frac{c}{\frac{25}{4}}\) = \(\frac{a-b+c}{3-5+\frac{25}{4}}\) = \(\frac{34}{\frac{17}{4}}\) = 8
\(\Rightarrow\) \(\begin{cases}a=24\\b=40\\c=50\end{cases}\)
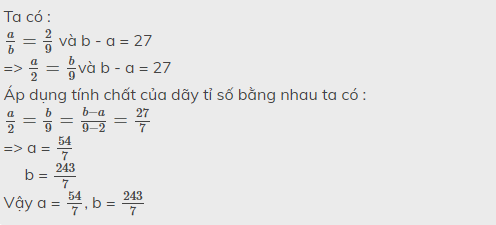
Theo bài ra ta có :
\(\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{4}}=\frac{c}{\frac{1}{6}}\)
Áp dụng dãy tỉ số bằng nhau ta có:
\(\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{4}}=\frac{c}{\frac{1}{6}}=\frac{a+b-c}{\frac{1}{3}+\frac{1}{4}-\frac{1}{6}}=-\frac{20}{\frac{5}{12}}=-48\)
=> a = -48 . 1/3 = -16
=> b = -48 . 1/4 = -12
=> c = -48 . 1/6 = -8