Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`f'(x) = x^2 - 4x+m`
`f'(x) >=0 <=>x^2-4x+m>=0`
`<=> \Delta' >=0`
`<=> 2^2-1.m>=0`
`<=> m<=4`
Vậy....

- TXĐ: D = R.
+ Với x = 1 ta có f ( 1 ) = k 2
+ Với x ≠ 1 ta có:
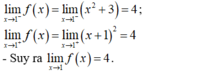
- Vậy để hàm số gián đoạn tại x = 1 khi và chỉ khi:
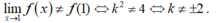
Chọn A

Chọn A.
Với x = 1 ta có f(1) = k2
Với x ≠ 1 ta có
![]()
suy ra ![]() .
.
Vậy để hàm số gián đoạn tại x = 1 khi ![]() ⇔ k2 ≠ 4 ⇔ k ≠ ±2.
⇔ k2 ≠ 4 ⇔ k ≠ ±2.

\(f'\left(x\right)=x^2-4\sqrt{2}x+8=\left(x-2\sqrt{2}\right)^2\)
\(f'\left(x\right)=0\Rightarrow\left(x-2\sqrt{2}\right)^2=0\Rightarrow x=2\sqrt{2}\)

Chọn B.
Ta có: 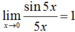 ; f(0) = a + 2.
; f(0) = a + 2.
Vậy để hàm số liên tục tại x = 0 thì a + 2 = 1 ⇔ a = -1.

Với a = 0, b = 1, hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{2x}&{{\rm{ }}x < 2}\\4&{{\rm{ }}x = 2}\\{ - 3x + 1}&{{\rm{ }}\,x > 2}\end{array}} \right.\)
Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( { - 3x + 1} \right) = - 3.2 + 1 = - 5\\\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {2x} \right) = 2.2 = 4\\ \Rightarrow \mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right)\end{array}\)
Do đó không tồn tại giới hạn \(\mathop {\lim }\limits_{x \to 2} f\left( x \right)\)
Vậy hàm số không liên tục tại x = 2.
b) Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( { - 3x + b} \right) = - 3.2 + b = - 6 + b\\\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {2x + a} \right) = 2.2 + a = 4 + a\\f\left( 2 \right) = 4\end{array}\)
Để hàm số liên tục tại x = 2 thì \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = f\left( 2 \right)\)
\( \Leftrightarrow - 6 + b = 4 + a = 4 \Leftrightarrow \left\{ \begin{array}{l}4 + a = 4\\ - 6 + b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = 10\end{array} \right.\)
Vậy với a = 0 và b = 10 thì hàm số liên tục tại x = 2.
c) Tập xác định của hàm số là: ℝ.
Với x < 2 thì \(f\left( x \right) = 2x + a\) là hàm đa thức nên liên tục.
Với x > 2 thì \(f\left( x \right) = -3x + b\) là hàm đa thức nên liên tục.
Do đó để hàm số liên tục trên ℝ thì hàm số \(f\left( x \right)\) liên tục tại x = 2.
Vậy với a = 0 và b = 10 thỏa mãn điều kiện.
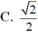
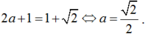
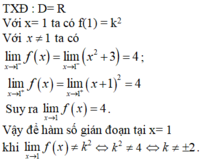
- Ta có:
- Vậy để hàm số có giới hạn khi:
Chọn C.