
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo đề bài ta có : UCLN(a,b)=18
=> a= 18m ; b = 18 n UCLN (m,n) = 1
ta có : a.b= BCNN(a,b).UCLN(a,b)=630.18=5670
=18m.18n=324.m.n=11340
=>m.n=11340:324=35
=>m,n thuộc U(35)={1,5,7,3}
lập bảng
| m | n | a | b |
| 1 | 35 | 18 | 630 |
| 5 | 7 | 90 | 126 |
| 7 | 5 | 126 | 90 |
| 35 | 1 | 630 | 18 |
vậy các cặp a,b thỏa mãn là (18,630);(90;126);(126;90);(630;18)
a. để B chia hết cho2,5,9 dư 1 thì A có tận cùng là 1.
khi đó ta có:x1831 chia2,5,9 dư 1
suy ra (x+1+8+3+1) chia 9 dư 1
suy ra x=6 và y =1


a)Để B chia hết cho 2;5
=>y =0
Thay vào ta được:x1830
Để B chia 9 dư 1 thì (x+1+8+3+0)chia 9 dư 1
=>(x+12)chia 9 dư 1
=>x=7

Em phải học hằng đảng thức lớp 8
Anh giải cho :
ta có:
<=> \(a^2-2ab+b+ab⋮9\)
<=> \(\left(a-b\right)^2+ab⋮9\)
=> \(\hept{\begin{cases}\left(a-b\right)^2⋮9\\ab⋮9\end{cases}}\)
Xét \(\left(a-b\right)^2⋮9\)
<=> \(\orbr{\begin{cases}a-b⋮3\\a-b⋮-3\end{cases}}\)
<=> \(\orbr{\begin{cases}\hept{\begin{cases}a⋮3\\b⋮3\end{cases}}\\\hept{\begin{cases}a⋮-3\Rightarrow a⋮3\\b⋮-3\Rightarrow b⋮3\end{cases}}\end{cases}}\left(1\right)\)
Xét \(ab⋮9\)
<=> \(\hept{\begin{cases}a⋮9\Rightarrow a⋮3\\b⋮9\Rightarrow b⋮3\end{cases}}\left(2\right)\)
Từ (1) và (2) => \(a⋮3\)
\(b⋮3\)
Answer:
Ta có:
\(a^2-ab+b^2⋮9⋮3\)
\(\Rightarrow a^2+2ab+b^2-3ab⋮3\)
\(\Rightarrow\left(a+b\right)^2-3ab⋮3\)
\(\Rightarrow\left(a+b\right)^2⋮3\)
\(\Rightarrow a+b⋮3\) (Vì 3 là số nguyên tố)
\(\Rightarrow\left(a+b\right)^2⋮9\)
Mà: \(a^2-ab+b^2=\left(a+b\right)^2-3ab⋮9\)
\(\Rightarrow3ab⋮9\Rightarrow ab⋮3\)
Do vậy: tồn tại ít nhất một trong hai số a hoặc b sẽ chia hết cho 3. Không mất tổng quát, ta giả sử a chia hết được cho 3
Lúc này: \(a.\left(a-b\right)⋮3\) mà \(a^2-ab+b^2=a.\left(a-b\right)+b^2⋮3\)

Lời giải:
Giả sử $a\geq b$. Vì $b+3\vdots a$ nên đặt $b+3=at$ với $t$ là số nguyên dương.
Vì $b=at-3< a$
$\Rightarrow a(t-1)< 3$
$\Rightarrow a(t-1)\leq 2$
Mà $a,t-1$ đều là số tự nhiên nên $a(t-1)\geq 0$
Vậy $a(t-1)=0$ hoặc $a(t-1)=1$ hoặc $a(t-1)=2$
TH1: $a(t-1)=0\Rightarrow t-1=0$ (do $a>0$
$\Rightarrow t=1$. Khi đó: $b+3=a$
$a+3\vdots b\Rightarrow b+3+b\vdots b\Rightarrow b+6\vdots b$
$\Rightarrow 6\vdots b\Rightarrow b\in \left\{1; 2; 3; 6\right\}$
Nếu $b=1$ thì $a=4$ (tm)
Nếu $b=2$ thì $a=5$ (tm)
Nếu $b=3$ thì $a=6$ (tm)
Nếu $b=6$ thì $a=9$ (tm)
TH2: $a(t-1)=1\Rightarrow a=t-1=1$
$\Rightarrow a=1; t=2$.
$b+3=at=2a=2\Rightarrow b=-1$ (vô lý => loại)
TH3: $a(t-1)=2\Rightarrow (a,t-1)=(1,2), (2,1)$
$\Rightarrow (a,t)=(1,3), (2,2)$
Nếu $a=1, t=3$ thì: $b+3=at=3a=3\Rightarrow b=0$ (loại)
Nếu $a=2; t=2$ thì $b+3=at=4\Rightarrow b=1$
Vậy $(a,b)=(4,1), (5,2), (6,3), (9,6), (1,2)$ và hoán vị.

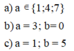
Do: \(\left(a+1\right)⋮b\Rightarrow a+1=kb\)
=> \(a=kb-1\)
=> \(\left(b+2\right)⋮kb-1\)
Do: \(b+2;kb-1>0\Rightarrow b+2\ge kb-1\Rightarrow b+3\ge kb\) (1)
NẾU: \(k\ge5\Rightarrow kb\ge5b=b+4b\ge b+4>b+3\) (2)
TỪ (1) VÀ (2) => LOẠI.
=> Nếu \(k=4\Rightarrow b+3\ge4b\Rightarrow1\ge b\Rightarrow b=1\) (DO \(b\ge1\left(b\inℕ^∗\right)\))
=> \(3⋮a\Rightarrow a=\left\{1;3\right\}\)
=> \(\hept{\begin{cases}a=1;b=1\\a=3;b=1\end{cases}}\)
NẾU k = 3 \(\Rightarrow b+3\ge3b\Rightarrow3\ge2b\Rightarrow b=1\)và kết quả giống tương tự TH1 k = 4
BẠN XÉT NỐT 2 TRƯỜNG HỢP k=1; k=2 nhaaaaaa