Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đường thẳng ax + by = -1 đi qua điểm A(-7; 4) nên tọa độ của A nghiệm đúng phương trình đường thẳng.
Ta có: a.(-7) + b.4 = -1
Khi đó ta có phương trình: 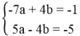
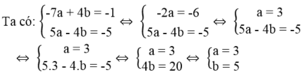
Vậy a = 3, b = 5.

a) (d) cắt (P) tại A => A thuộc d và (P)
xA= 3; A \(\in\) d=> yA = -xA - \(\frac{3}{2}\) => yA = -3 - \(\frac{3}{2}\) = \(\frac{-9}{2}\)
Mặt khác, A \(\in\) (P) => yA = axA2 => \(\frac{-9}{2}\) = a. 32 => a = \(\frac{-9}{2}\): 9 = \(\frac{-1}{2}\)
Vậy (P) có dạng y = \(\frac{-1}{2}\).x2
+) Vẽ đồ thị:
| x | -2 | -1 | 0 | 1 | 2 |
| y | -2 | \(\frac{-1}{2}\) | 0 | \(\frac{-1}{2}\) | -2 |
(P) đí qua 4 điểm (-2;-2); (-1;\(\frac{-1}{2}\)); (0;0); (1;\(\frac{-1}{2}\)); (2;-2)
b) Phương trình hoành độ giao điểm: \(\frac{-1}{2}\).x2 = - x - \(\frac{3}{2}\)
<=> -x2 + 2x + 3 = 0
<=> x = -1 hoặc x = 3 (Vì a - b + c = -1 - 2 + 3 = 0)
=> xB = -1 => yB = \(\frac{-1}{2}\).(-1)2 = \(\frac{-1}{2}\)
Vậy B (-1;\(\frac{-1}{2}\))

Vì đường thẳng ax-by=4 đi qua 2 điểm A(4;3) và B(-6;-7)
nên 4a-3b=4 và -6a-(-7)b=4
3(4a-3b)=12 và 2(-6a+7b)=8
12a-9b=12 và -12a+14b=8
5b=20 và 4a-3b=4
b=4 và a=4

a) Đồ thị hàm số y = ax + b đi qua A(1; 3) và B(-1; -1)
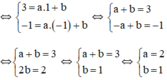
Vậy a = 2; b = 1; hàm số y = 2x + 1.
b) y = ax + b song song với y = x + 5
⇒ a = 1.
Đồ thị hàm số đi qua C(1; 2) ⇔ 2 = a.1 + b ⇔ a + b = 2 ⇒ b = 1.
Vậy a = 1; b = 1.