HL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 5 2016
=> 72 - 20x - 36x - 84 = 30x - 240 - 6x + 84
=> (72 - 84 ) - (20x + 36x ) = (30x - 6x ) - 240 + 84
=> -12 - 56x = 24x - 156
=> -12 + 156 = 24x + 56x
=> 144 = 80x
=> x = 144 : 80
=> x = 9/5
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 9 2021
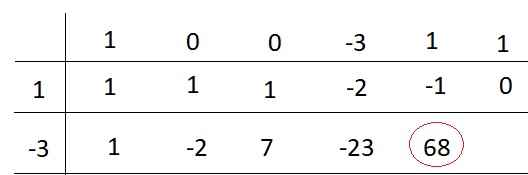
Nếu thực hiện chia theo lược đồ Hoocne thì kết quả như thế này:
\(f\left(x\right)=\left(x^2+2x-3\right)\left(x^3-2x^2+7x-23\right)+68\)
Hay \(f\left(x\right)\) chia \(x^2+2x-3\) được thương \(x^3-2x^2+7x-23\) và dư \(68\)
7 tháng 6 2016
\(=x^4-xy+xy+x^2y-x^4-x^2y+3xy-xy.\)
\(=2xy\)
Thay x = 1/4 , y = - 2005 ta được: 2xy = 2.1/4 . ( - 2005 ) = -2005/2
8 tháng 6 2016
\(A=x\left(x^3-y\right)+xy+x^2\left(y-x^2\right)-y\left(x^2-3x\right)-yx=\)
\(=x^4-xy+xy+x^2y-x^4-yx^2+3xy-xy=2xy\)
Với \(x=\frac{1}{4};y=-2005\)thì \(A=2\cdot\frac{1}{4}\cdot\left(-2005\right)=-\frac{2005}{2}\)
TN
25 tháng 7 2016
Bài 1:
a) A= x2 + 4x + 5
=x2+4x+4+1
=(x+2)2+1\(\ge\)0+1=1
Dấu = khi x+2=0 <=>x=-2
Vậy Amin=1 khi x=-2
b) B= ( x+3 ) ( x-11 ) + 2016
=x2-8x-33+2016
=x2-8x+16+1967
=(x-4)2+1967\(\ge\)0+1967=1967
Dấu = khi x-4=0 <=>x=4
Vậy Bmin=1967 <=>x=4
Bài 2:
a) D= 5 - 8x - x2
=-(x2+8x-5)
=21-x2+8x+16
=21-x2+4x+4x+16
=21-x(x+4)+4(x+4)
=21-(x+4)(x+4)
=21-(x+4)2\(\le\)0+21=21
Dấu = khi x+4=0 <=>x=-4
b)đề sai à
S
26 tháng 7 2016
ài 1:
a) A= x2 + 4x + 5
=x2+4x+4+1
=(x+2)2+1$\ge$≥0+1=1
Dấu = khi x+2=0 <=>x=-2
Vậy Amin=1 khi x=-2
b) B= ( x+3 ) ( x-11 ) + 2016
=x2-8x-33+2016
=x2-8x+16+1967
=(x-4)2+1967$\ge$≥0+1967=1967
Dấu = khi x-4=0 <=>x=4
Vậy Bmin=1967 <=>x=4
Bài 2:
a) D= 5 - 8x - x2
=-(x2+8x-5)
=21-x2+8x+16
=21-x2+4x+4x+16
=21-x(x+4)+4(x+4)
=21-(x+4)(x+4)
=21-(x+4)2$\le$≤0+21=21
Dấu = khi x+4=0 <=>x=-4
b)đề sai à
13 tháng 9 2016
làm như bình thường là đc:
a) ( x + 2 )^3 - x^2 . ( x+ 6 ) - 8
= ( x^3 + 3.x^2.2 +3.x.2^2 + 2^3 ) - ( x^3 + 6x^2 ) - 8
= x^3 + 6x^2 + 12x + 8 - x^3 - 6x^2 - 8
=12x
b) ( x - 2 ) . ( x^2 + 2x + 4 ) - ( x^3 + 2 )
= x^3 - 2^3 - ( x^3 + 2 )
= x^3 - 8 - x^3 - 2
= -6
(x-2)(x+2)(x+4) = (x^2 - 4) (x+4) = x^3 + 4x^2 -4x - 16