Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bằng máy tính cầm tay, ta tính được kết quả là: \(\sqrt[3]{{15}}:5 - 2 \approx - 1,51\)

Đối với máy tính CASIO fx–500 MS ta ấn như sau:
 (để ra kết quả).
(để ra kết quả).
 (để lấy kết quả đến 4 chữ số thập phân)
(để lấy kết quả đến 4 chữ số thập phân)
Kết quả: 51139,3736.

Nếu dùng máy tính CASIO fx-500 MS ta làm như sau.
Ấn 
Ấn liên tiếp phím  cho đến khi màn hình hiện ra
cho đến khi màn hình hiện ra
Ấn liên tiếp  để lấy 4 chữ số ở phần thập phân. Kết quả hiện ra trên màn hình là 8183.0047.
để lấy 4 chữ số ở phần thập phân. Kết quả hiện ra trên màn hình là 8183.0047.

b) \(\sqrt{7-2\sqrt{10}}-\sqrt{7+2\sqrt{10}}\)
\(=\sqrt{5-2\cdot\sqrt{5}\cdot\sqrt{2}+2}-\sqrt{5+2\cdot\sqrt{5}\cdot\sqrt{2}+2}\)
\(=\sqrt{\left(\sqrt{5}-\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{5}+\sqrt{2}\right)^2}\)
\(=\left|\sqrt{5}-\sqrt{2}\right|-\left|\sqrt{5}+\sqrt{2}\right|\)
\(=\sqrt{5}-\sqrt{2}-\sqrt{5}-\sqrt{2}\) (vì \(\sqrt{5}\ge\sqrt{2}\)
=0
c) \(\sqrt{4-2\sqrt{3}}+\sqrt{4+2\sqrt{3}}\)
\(=\sqrt{3-2\sqrt{3}+1}+\sqrt{3+2\sqrt{3}+1}\)
\(=\sqrt{\left(\sqrt{3}-1\right)^2}+\sqrt{\left(\sqrt{3}+1\right)^2}\)
\(=\left|\sqrt{3}-1\right|+\left|\sqrt{3}+1\right|\)
\(=\sqrt{3}-1+\sqrt{3+1}\) (vì \(\sqrt{3}\ge1\))
\(=2\sqrt{3}\)
a)\(\sqrt{5+2\sqrt{6}}-\sqrt{5+2\sqrt{6}}\)
\(=\sqrt{3+2\cdot\sqrt{3}\cdot\sqrt{2}+2}-\sqrt{3-2\cdot\sqrt{3}\cdot\sqrt{2}+2}\)
\(=\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}\)
\(=\left|\sqrt{3}+\sqrt{2}\right|-\left|\sqrt{3}-\sqrt{2}\right|\)
\(=\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2}\) (vì \(\sqrt{3}\ge\sqrt{2}\))
=0

a/ ĐKXĐ: ...
\(\Leftrightarrow x+8+\sqrt{x+8}-\left(x+8\right)=\sqrt{x}+\sqrt{x+3}\)
\(\Leftrightarrow\sqrt{x+8}=\sqrt{x}+\sqrt{x+3}\)
\(\Leftrightarrow x+8=2x+3+2\sqrt{x^2+3x}\)
\(\Leftrightarrow5-x=2\sqrt{x^2+3x}\) (\(x\le5\))
\(\Leftrightarrow x^2-10x+25=4\left(x^2+3x\right)\)
\(\Leftrightarrow...\)
b/ ĐKXĐ: \(2\le x\le5\)
\(\Leftrightarrow2\left(x-2\right)+\sqrt{2\left(x-2\right)}\left(\sqrt{5-x}-\sqrt{3x-3}\right)=0\)
\(\Leftrightarrow\sqrt{2\left(x-2\right)}\left(\sqrt{2x-4}+\sqrt{5-x}-\sqrt{3x-3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\\sqrt{2x-4}+\sqrt{5-x}=\sqrt{3x-3}\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow x+1+2\sqrt{\left(2x-4\right)\left(5-x\right)}=3x-3\)
\(\Leftrightarrow\sqrt{\left(2x-4\right)\left(5-x\right)}=x-2\)
\(\Leftrightarrow\left(2x-4\right)\left(5-x\right)=\left(x-2\right)^2\)
\(\Leftrightarrow...\)
c/ ĐKXĐ: \(x\le12\)
\(\Leftrightarrow\sqrt[3]{24+x}\sqrt{12-x}-6\sqrt{12-x}+12-x=0\)
\(\Leftrightarrow\sqrt{12-x}\left(\sqrt[3]{24+x}-6+\sqrt{12-x}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=12\\\sqrt[3]{24+x}+\sqrt{12-x}=6\left(1\right)\end{matrix}\right.\)
Xét (1):
Đặt \(\left\{{}\begin{matrix}\sqrt[3]{24+x}=a\\\sqrt{12-x}=b\ge0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=6\\a^3+b^2=36\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=6-a\\a^3+b^2=36\end{matrix}\right.\)
\(\Leftrightarrow a^3+\left(6-a\right)^2=36\)
\(\Leftrightarrow a^3+a^2-12a=0\)
\(\Leftrightarrow a\left(a^2+a-12\right)=0\Rightarrow\left[{}\begin{matrix}a=0\\a=3\\a=-4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt[3]{24+x}=0\\\sqrt[3]{24+x}=3\\\sqrt[3]{24+x}=-4\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}24+x=0\\24+x=27\\24+x=-64\end{matrix}\right.\)



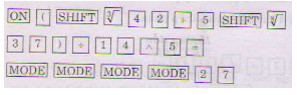


a) \({4^6}.\sqrt {0,1} = 1295,2689\)
b) \(\sqrt[8]{{2,{1^{18}} + 1}} - \sqrt {2,{1^{12}} + 1} = - 80,4632\)
c) \(\frac{{1,{5^3}}}{{\sqrt[3]{{6,8}}}} = 1,7814\)