Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\( i = \frac{\lambda D}{a}= 0,64 mm.\)
Số vân tối quan sát được trên màn là
\(N_t = 2.[\frac{L}{2i}+0,5]=2.9=18.\)

\(i = \frac{\lambda D}{a}=\frac{0,5.2}{0,5}= 2mm.\)
Số vân sáng trên màn quan sát là
\(N_s= 2.[\frac{L}{2i}]+1 =2.6+1 = 13.\)

Tịnh tiến màn quan sát lại gần mặt phẳng chưa hai khe 25 cm tức là \(D' = D-0,25.\)
\(i_1 = \frac{\lambda D}{a}\\
i_2 =\frac{\lambda (D-0,25)}{a} \)=> \(\frac{i}{i'}= \frac{D}{D-0,25}= \frac{5}{4}\)
=> \(D = 5.0,25 = 1,25m.\)
=> \(\lambda = \frac{i.a}{D}= 0,48 \mu m.\)
Chú ý là giữ nguyên đơn vị i (mm); a (mm) ; D (m) thì đơn vị bước sóng \(\lambda (\mu m)\).

Vân sáng bậc 4 cách vân trung tâm là
\(x_ 4 = 4.i = 4.\frac{\lambda D}{a} = 3,2mm.\)
Chú ý nếu giữ nguyênđơn vị của \(\lambda (\mu m)\), D(m), a(mm) thì khi đó kết quả cho \(x\) ra đơn vị là mm.

Chọn C
Ta có: i = λD/a = 2mm.
Số vân sáng trên màn là:
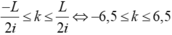
=> Có 13 giá trị của k thỏa mãn
Vậy trên màn có 13 vân sáng

Chọn C
Ta có i=1,1 mm.
L/2i = 7,7 =>
Trên màn có 15 vân sáng và 16 vân tối.


\(i =\frac{\lambda D}{a} =\frac{0,64.2,4}{0,8}=1,92mm. \)
Số vân sáng trên màn là
\(N_s= 2.[\frac{L}{2.i}]+1=2.[\frac{4,8.10^{-2}}{2.1,92.10^{-3}}]+1 = 25.\)
a