KP
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
9 tháng 6 2023
X = {5; 7; 9; 11; 13;...;83}
Xét dãy số: 5; 7; 9;11; 13;...; 83
Dãy số trên là dãy số cách đều có khoảng cách là: 7 - 5 = 2
Phần tử thứ 11 của tập hợp X chính là số hạng thứ 11 của dãy số trên
Áp dụng công thức tính số thứ n của dãy số cách đều:
Stn = số đầu + khoảng cách \(\times\)(n-1)
Số thứ 11 của dãy số trên là: 5 + 2 \(\times\) ( 11 - 1) = 25
Kết luận:
Phần tử đứng thứ 11 tính từ trái qua phải của tập hợp X khi các phần tử của tập hợp X được sắp xếp theo thứ tự từ bé đến lớn là: 25
21 tháng 6 2023
a: -10/8<-1
-19/19=-1
-1<-2/10<0
0<5/12<1<17/15
=>17/15>1>5/12>-2/10>-19/19>-10/8
b: -1/3=-4/12; -5/12=-5/12; -3/4=-9/12; -1/4=-3/12; -7/12=-7/12
=>-3/4<-7/12<-5/12<-1/3<-1/4
VN
0
13 tháng 12 2023
\(\sqrt{16}=4;\dfrac{2}{3}=0,\left(6\right);\Omega=3,14;-\sqrt{5}\simeq-2,24\)
\(-5,6< -2,23< 0\)
=>\(-5,6< -\sqrt{5}< 0\)(1)
\(0< \dfrac{2}{3}< 3,14< 4\)
=>\(0< \dfrac{2}{3}< \Omega< \sqrt{16}\)(2)
Từ (1) và (2) suy ra \(-5,6< -\sqrt{5}< 0< \dfrac{2}{3}< \Omega< \sqrt{16}\)
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
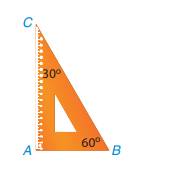
- AB < AC < BC nên sắp xếp độ dài các cạnh theo thứ tự từ bé đến lớn là: AB, AC, BC.
\(\widehat C < \widehat B < \widehat A\) nên sắp xếp độ lớn các góc theo thứ tự từ bé đến lớn là: \(\widehat C;\widehat B;\widehat A\)
- Góc lớn nhất là góc A đối diện với cạnh BC. Góc bé nhất là góc C đối diện với cạnh AB.
14 tháng 7 2023
\(2^{100}=2^{4.25}=16^{25}\)
\(3^{75}=3^{3.25}=27^{25}\)
\(5^{50}=5^{2.25}=25^{25}\)
vì \(16^{25}< 25^{25}< 27^{25}\)
⇒ \(2^{100}< 5^{50}< 3^{75}\)
Tập hợp F : { 5;7;9;11;13;................;81;83;85}