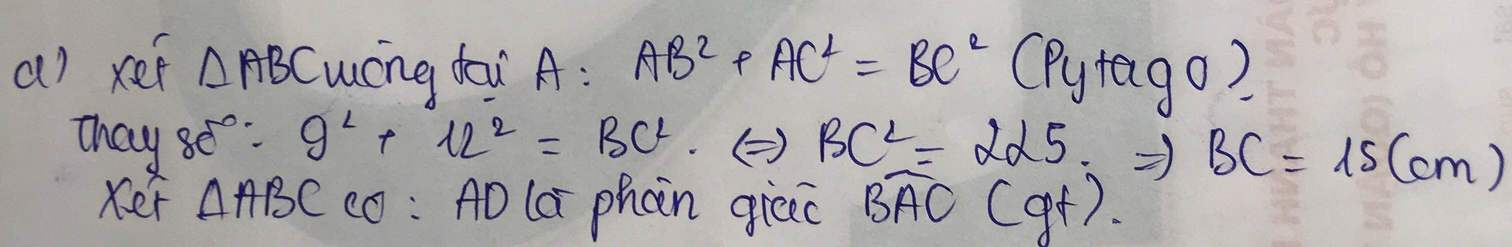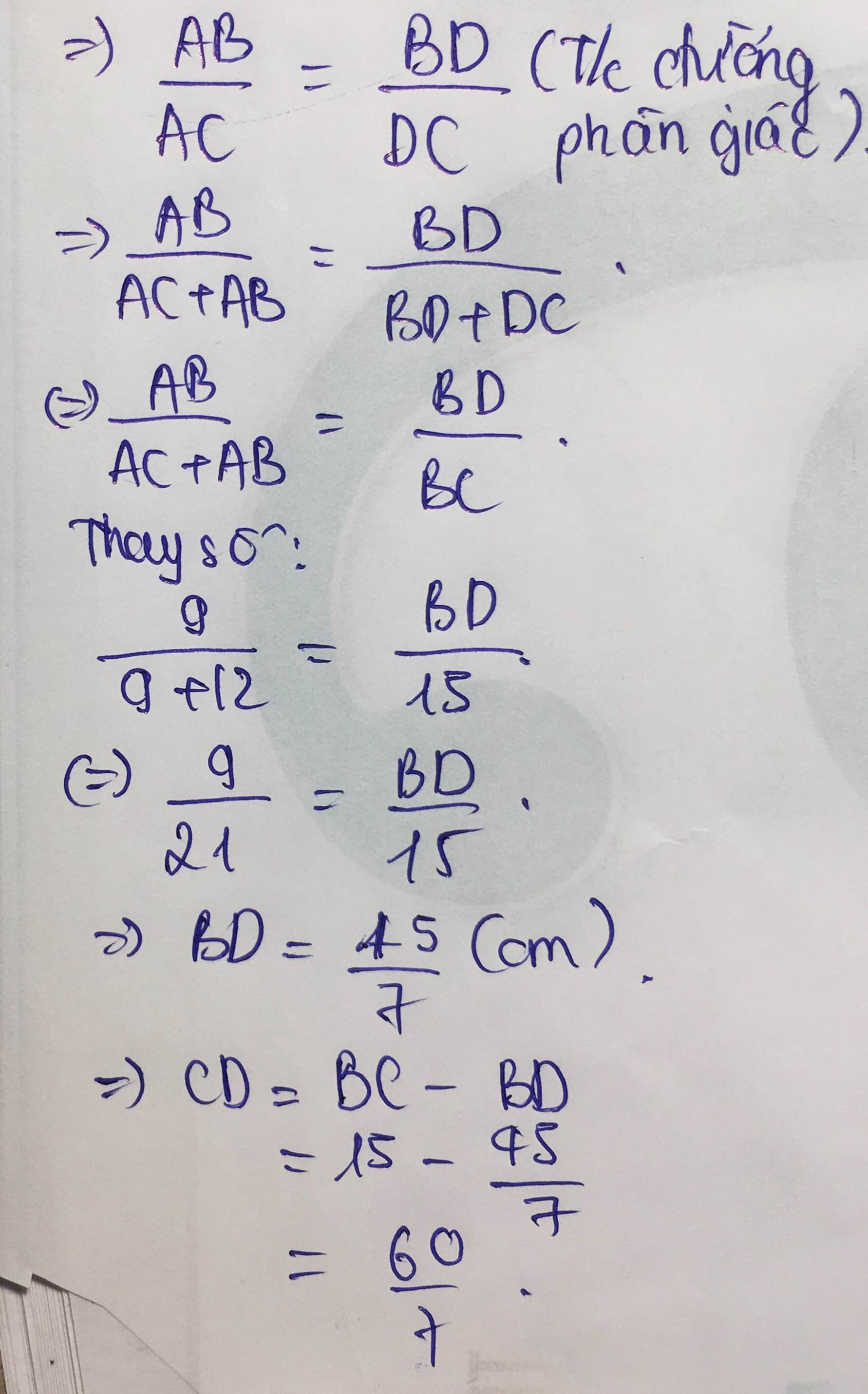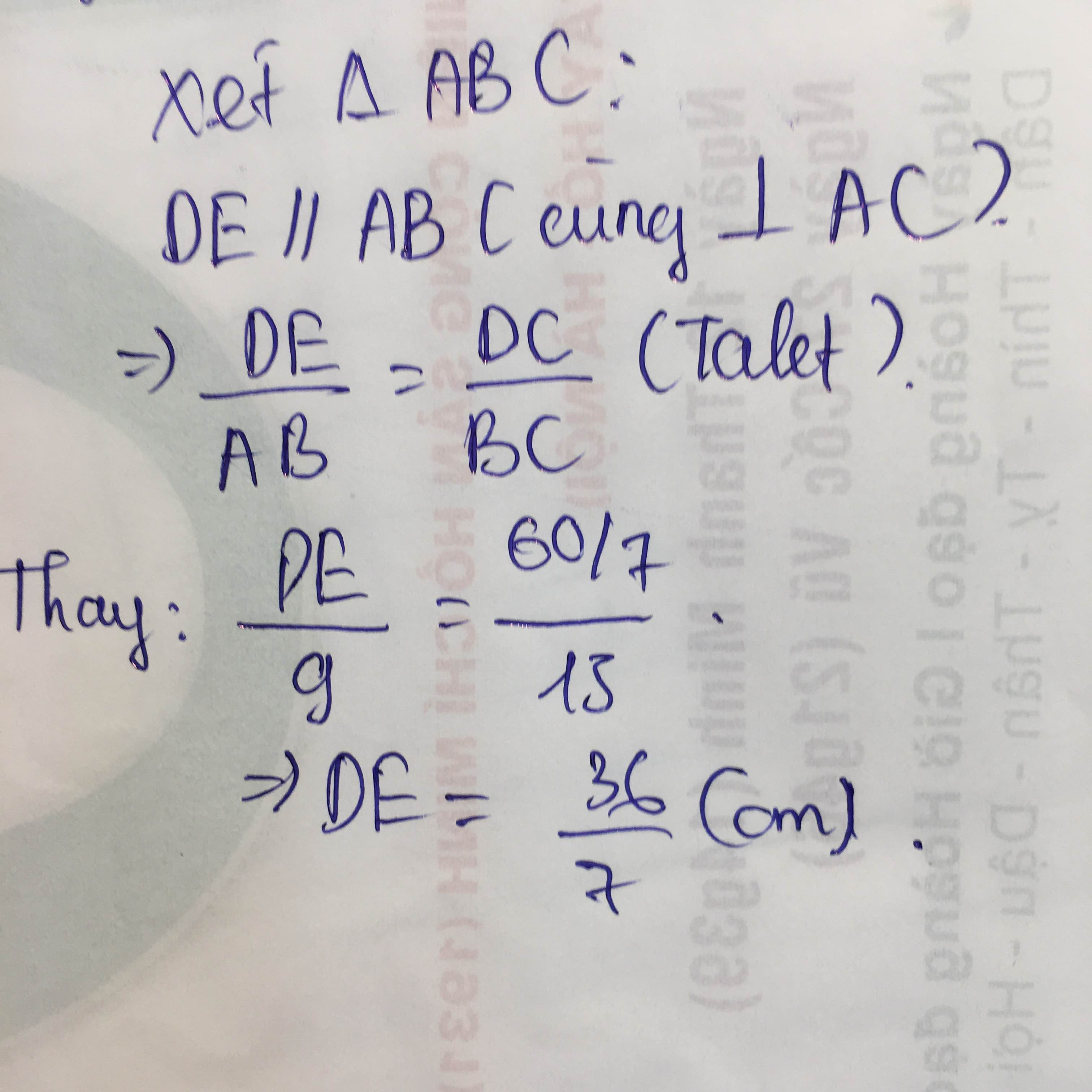Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E
a) Ra có tam giác ABC vuông tại A ( gt )
\(\Rightarrow BC^2=AB^2+AC^2=9^2+12^2=81+144=225\left(cm\right)\)
\(\Rightarrow BC=15\left(cm\right)\)
Vì AD là tia phân giác của \(\widehat{BAC}\)( gt )
\(\Rightarrow\frac{DC}{DB}=\frac{AC}{AB}=\frac{12}{9}=\frac{4}{3}\Rightarrow\frac{DC+DB}{DB}=\frac{4+3}{3}=\frac{7}{3}\)\(\Rightarrow\frac{BC}{DB}=\frac{7}{3}\)
\(\Rightarrow DB=\frac{3}{7}.BC=\frac{3}{7}.15=\frac{45}{7}\left(cm\right)\)
\(\Rightarrow DC=15-\frac{45}{7}=\frac{60}{7}\left(cm\right)\)
Ta có DE // AB ( Vì AB và DE vuông góc với AC )
Áp dụng hệ quả định lý Ta lét ta có:
\(\Rightarrow\frac{DE}{AB}=\frac{CD}{CB}=\frac{60}{\frac{7}{15}}=\frac{4}{7}\)\(\Rightarrow DE=\frac{4}{7}.AB=\frac{4}{7}.9=\frac{36}{7}\left(cm\right)\)
b) Ta có: \(S_{ADC}=\frac{1}{2}.DE.AC=\frac{1}{2}.\frac{36}{7}.12=\frac{216}{7}\left(cm^2\right)\)
Ta có: \(S_{ABC}=\frac{1}{2}.AB.AC=\frac{1}{2}.9.12=54\left(cm^2\right)\)
\(\Rightarrow S_{ABD}=S_{ABC}-S_{ACD}=54-\frac{216}{7}=\frac{126}{7}\left(cm^2\right)\)

a. Áp dụng định lý pitago vào tam giác vuông ABC, có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{9^2+12^2}=\sqrt{225}=15cm\)
Áp dụng t/c tia phân giác góc A, ta có:
\(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)
\(\Leftrightarrow\dfrac{9}{12}=\dfrac{BD}{CD}\) \(\Leftrightarrow\dfrac{3}{4}=\dfrac{BD}{CD}\) \(\Leftrightarrow\dfrac{CD}{4}=\dfrac{BD}{3}\)
Áp dụng t/c dãy tỉ số bằng nhau, ta có:
\(\dfrac{CD}{4}=\dfrac{BD}{3}=\dfrac{CD+BD}{4+3}=\dfrac{15}{7}\)
\(\Rightarrow CD=\dfrac{15}{7}.4=\dfrac{60}{7}cm\)
\(\Rightarrow BD=\dfrac{15}{7}.3=\dfrac{45}{7}cm\)
Xét tam giác ABD và tam giác ADE có:
\(\widehat{E}=\widehat{D}=90^0\)
AD: cạnh chung
\(\widehat{BAD}=\widehat{DAE}\) ( gt )
=> tam giác ABD = tam giác ADE ( c.g.c )
=> BD = ED = \(\dfrac{45}{7}cm\)
b. Xét tam giác ABD và tam giác ABC, có:
\(\widehat{BAC}=\widehat{BDA}=90^0\)
\(\widehat{B}:chung\)
Vậy tam giác ABD đồng dạng tam giác ABC ( g.g )
\(\Rightarrow\dfrac{BD}{AB}=\dfrac{AD}{AC}\)
\(\Leftrightarrow\dfrac{45}{\dfrac{7}{9}}=\dfrac{AD}{12}\)
\(\Leftrightarrow\dfrac{5}{7}=\dfrac{AD}{12}\)
\(\Leftrightarrow7AD=60\Leftrightarrow AD=\dfrac{60}{7}cm\)
\(S_{ABD}=\dfrac{1}{2}.BD.AD=\dfrac{1}{2}.\dfrac{45}{7}.\dfrac{60}{7}\simeq27,55cm^2\)
\(S_{ACD}=\dfrac{1}{2}.CD.AD=\dfrac{1}{2}.\dfrac{60}{7}.\dfrac{60}{7}\simeq36,73cm^2\)

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=9^2+12^2=225\)
hay BC=15(cm)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{BD}{9}=\dfrac{CD}{12}\)
mà BD+CD=BC(D nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{9}=\dfrac{CD}{12}=\dfrac{BD+CD}{9+12}=\dfrac{BC}{21}=\dfrac{15}{21}=\dfrac{5}{7}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{BD}{9}=\dfrac{5}{7}\\\dfrac{CD}{12}=\dfrac{5}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BD=\dfrac{45}{7}cm\\CD=\dfrac{60}{7}cm\end{matrix}\right.\)
Vậy: \(BD=\dfrac{45}{7}cm;CD=\dfrac{60}{7}cm\)