Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha
Xét hai \(\Delta\) vuông ABE và HBE có:
BE là cạnh huyền chung
\(\widehat{ABE}=\widehat{HBE}\left(gt\right)\)
Vậy \(\Delta ABE=\Delta HBE\left(ch-gn\right)\)
b) ΔABC vuông tại A
\(\Rightarrow\widehat{ABC}+\widehat{ACB}=90^o\)
Mà \(\widehat{ABC}=60^o\)
\(\Rightarrow\widehat{ACB}=30^o\)
ΔEHC vuông tại H
\(\Rightarrow\widehat{HEC}+\widehat{HCE}=90^o\)
Mà \(\widehat{HCE}=30^o\)
\(\Rightarrow\widehat{HEC}=60^o\left(1\right)\)
Ta lại có : \(\widehat{ABE}=\widehat{EBH}=\frac{\widehat{ABC}}{2}=\frac{60^o}{2}=30^o\)
ΔBEH vuông tại H
\(\widehat{EBH}+\widehat{BEH}=90^o\)
Mà \(\widehat{EBH}=30^o\)
\(\Rightarrow\widehat{BEH}=60^o\)
Vì HK // BE
\(\Rightarrow\widehat{BEH}=\widehat{EHK}\) (2 góc so le trong bằng nhau)
Mà \(\widehat{BEH}=60^o\)
nên \(\widehat{EHK}=60^o\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\)ΔEHK là tam giác đều
c) Xét hai tam giác vuông AEM và HEC có:
AE = HE (ΔABE=ΔHBE)
\(\widehat{AEM}=\widehat{HEC}\) (2 góc đối đỉnh)
Vậy: ΔAEM=ΔHEC(cgv−gn)
\(\Rightarrow\)AM = HC (hai cạnh tương ứng)
Ta có: BM = BA + AM
BC = BH + HC
Mà BA = BH (ΔABE=ΔHBE)
AM = HC (cmt)
⇒ BM = BC
⇒ΔBMC cân tại B
⇒ BN là đường phân giác đồng thời là đường trung tuyến của \(\Delta\) BMC
Nên NM = NC
tự vẽ hình bn nha
a) vì BE là p/g của góc B =>góc B1=góc B2
xét tam giác ABE vg tại A và tam giác HBE vg tại H có :
BE chung
góc B1=góc B2( cmt)
=> tam giác ABE = tam giác HBE ( ch-gn)
nhớ tick cho mk

Bạn tự vẽ hình nha.
a,Xét tg ABE và tg HBE:
^BAE=^BHE=90*
^ABE=^HBE(BE là pg)
BE chung
=>tg ABE= tg HBE(ch-gn)
b,+,tg ABC có:^BAC=90*,^ABC=60*
=>^C=30*
+,tg BHE có: ^BHE=90*,^EBH=30*(^EHB=1/2ABC)
=>^HEB=60*
Mà HK // BE
=>^HBE=^EHK=60*(slt)
+, tg CHE có:^EHC=90*,^C=30*
=>HEC=60*
+,tg HEK có:
^EHK=60*,^HEC(^HEK)=60*
=>TG HEK đều(dhnb)
Phần c mik chỉ ghi các bước thôi còn bạn tự chình bày nhé.
c, +,CM:tg AEM=tg HEC(cgv-gnk)
=>AM=HC
+,CM:BM=BC
+,CM:tg BMI=tgBCI(cgc)
=>NM=NC
Xong r nha. Chúc bạn học tốt.

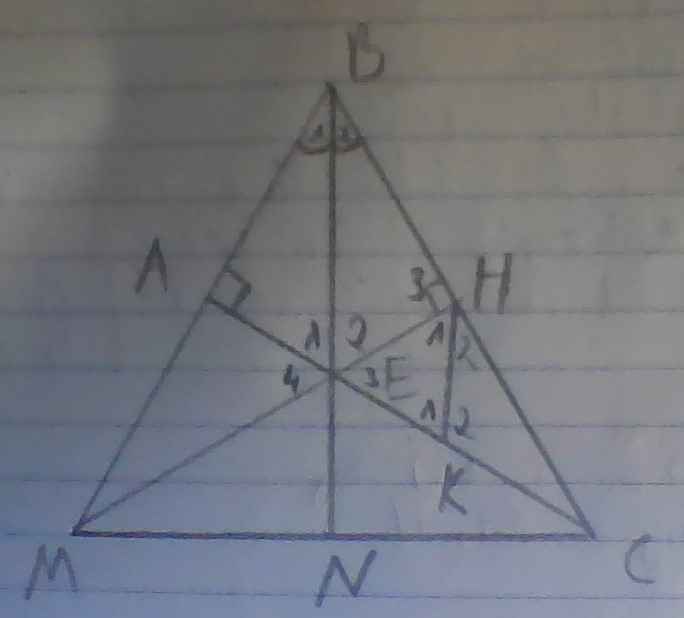
a) có BE là tia p/g của góc ABC
=> góc B1 = góc B2 = góc ABC/2 = 600 /2 = 300
có △ABC vuông tại A => △ABE vuông tại A
EH⊥BC=> △HBE vuông tại H
Xét △ vuông ABE và △vuông HBE có
góc B1 = góc B2
BE chung
=>△ vuông ABE =△vuông HBE ( cạnh huyền - góc nhọn)
b) có △ABE vuông tại A=> góc B1 + góc E1 = 900
góc E1 = 600 ( vì góc B1 = 300)
có △ vuông ABE =△vuông HBE
=> góc E1 = góc E2
mà HK//BE => góc E1 = góc K1 (ĐV)
và góc E2 = góc H1 (SLT)
=> góc E1 = góc E2 = góc K1=góc H1 = 600
=> △HEK đều
c) có góc E1 = góc E2 ; góc E3 = góc E4
=>góc E1 +góc E4 = góc E2 + góc E3
=> góc BEM= góc BEC
Xét △BEM và △ BEC có
góc B1 = góc B2
BE chung
góc BEM= góc BEC
=> △BEM = △ BEC (g.c.g)
=>BM=BC
=>△BMC cân tại B
trong △BMC có BN là đường p/g xuất phát từ đỉnh B
lại có △BMC cân tại B
=> BN cũng là đường trung tuyến xuất phát từ đỉnh B
=> N là trung điểm của MC
=> NM=NC

Câu a
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau

a) Xét \(\Delta ABC\) có:
\(AB=AC\left(gt\right)\)
=> \(\Delta ABC\) cân tại A.
=> \(\widehat{ABC}=\widehat{ACB}\) (tính chất tam giác cân).
b) Ta có: \(\widehat{ABC}=\widehat{ACB}\left(cmt\right)\)
Mà \(\widehat{ECK}=\widehat{ACB}\) (vì 2 góc đối đỉnh).
=> \(\widehat{ABC}=\widehat{ECK}.\)
Hay \(\widehat{DBH}=\widehat{ECK}.\)
Xét 2 \(\Delta\) vuông \(DBH\) và \(ECK\) có:
\(\widehat{DHB}=\widehat{EKC}=90^0\left(gt\right)\)
\(DB=EC\left(gt\right)\)
\(\widehat{DBH}=\widehat{ECK}\left(cmt\right)\)
=> \(\Delta DBH=\Delta ECK\) (cạnh huyền - góc nhọn).
=> \(DH=EK\) (2 cạnh tương ứng).
c) Xét 2 \(\Delta\) vuông \(DHI\) và \(EKI\) có:
\(\widehat{DHI}=\widehat{EKI}=90^0\)
\(DH=EK\left(cmt\right)\)
\(\widehat{DIH}=\widehat{EIK}\) (vì 2 góc đối đỉnh)
=> \(\Delta DHI=\Delta EKI\) (cạnh góc vuông - góc nhọn kề).
=> \(DI=EI\) (2 cạnh tương ứng).
=> \(I\) là trung điểm của \(DE\left(đpcm\right).\)
Chúc bạn học tốt!
Bài 1:
a) Sai đề rồi bạn, đáng lý ra phải là AB=AF mới đúng
Xét ΔABE vuông tại E(AD⊥BE) và ΔAFE vuông tại E(AD⊥BE,F∈BE) có
AE chung
\(\widehat{BAE}=\widehat{FAE}\)(do AE là tia phân giác của góc A)
Do đó: ΔABE=ΔAFE(cạnh góc vuông, góc nhọn kề)
⇒AB=AF(hai cạnh tương ứng)
b) Xin lỗi bạn, mình chỉ biết làm theo cách lớp 8 thôi nhé
Xét tứ giác HFKD có HF//DK(do HF//BC,D∈BC) và HF=DK(gt)
nên HFKD là hình bình hành(dấu hiệu nhận biết hình bình hành)
⇒HD//KF và HD=KF(hai cạnh đối trong hình bình hành HFKD)
c)
Xét ΔABC có AB<AC(gt)
mà góc đối diện với cạnh AB là góc C
và góc đối diện với cạnh AC là góc B
nên \(\widehat{C}< \widehat{B}\)(định lí về quan hệ giữa cạnh và góc đối diện trong tam giác)
hay \(\widehat{ABC}>\widehat{C}\)(đpcm)
Bạn tự vẽ hình nha
a) CM: tam giác ABE = tam giác HBE
Xét tam giác ABE (Â=90o) và tam giác HBE (góc H= 90o), ta có:
Góc ABE = Góc HBE ( BE là p/g góc B)
BE là cạnh chung
Vậy: tam giác ABE = tam giác HBE ( cạnh huyền-góc nhọn)
c) CM: NM=NC
Xét tam giác AEM và tam giác HEC, ta có:
góc AEM = góc HEC ( đối đỉnh)
AE = HE (tam giác ABE = tam gác HBE)
góc EAM = góc EHC = 90o
Vậy: tam giác AEM = tam giác HEC (g-c-g)
Ta có: AB+AM=BM
BH+HC=BC
mà BA=BH(tam giác BAE= tam giác BEH)
AM=HC(tam giác AEM= tam giác HEC)
nên BM=BC
Xét tam giác NBM và tam giác NBC, ta có:
NB là cạnh chung
góc NBM= góc NBC ( BE là p/g góc B)
BM=BC (cmt)
Vậy tam giác NBM= tam giác NBC ( c-g-c)
=> NM=NC ( 2 cạnh tương ứng)
Sorry vì mình khong làm được bài b