
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 1) Vì B = 30°
=》sinB = 1/2 (tính chất )
=》cosB = \(\sqrt{ }\)3/2 ( tính chất )
=》 tanB = \(\sqrt{ }\)3/3( tính chất )
=》 cotB = \(\sqrt{ }\)3( tính chất )
Lại có B + C = 90°
=》 sinB = cosC = 1/2
=》 cosB = sinC = \(\sqrt{ }\)3/2
=》tanB = cotC = \(\sqrt{ }\)3/3
=》cotB = tanC = \(\sqrt{ }\)3
SinA = BC/BC = 1
CosA có thể bằng AB/BC hay AC/BC (loại)
TanA có thể bằng BC/AB hay BC/AC (loại)
CotA có thể bằng AB/BC hay AC/BC (loại)
Bài 2) Vì \(\Delta\)MNP vuông cân tại M
=》 MN = MP = b
Áp dụng định lý Py ta go vào \(\Delta\)ABC có :
NM2 +MP2 = NP2
=》 NP2 =b2 + b2 =2b2
=》NP = \(\sqrt{ }\)2b2
SinN = MP/NP = b/\(\sqrt{ }\)2b2 = \(\sqrt{ }\)2/2
CosN = NM/NP = b/\(\sqrt{ }\)2b2 = \(\sqrt{ }\)2/2
TanN = MP/NM = b/b =1
CotN = NM/MP = b/b = 1
Vì N + P =90°
=》sinN = cosP = \(\sqrt{ }\)2/2
=》cosN = sinP =\(\sqrt{ }\)2/2
=》tanN = cotP = 1
=》cotN = tanP = 1

a) A,D,C C (O;AD)
=> DC _|_ CA
b) A,B,D C (O;AD)
=> BD _|_ AB
\(\Rightarrow\hept{\begin{cases}BD//CH\left(\perp AB\right)\\BH//CD\left(\perp AC\right)\end{cases}}\)
=> BHCD là hình bình hành
\(\Rightarrow\hept{\begin{cases}BH=DC\\BD=HC\end{cases}}\)
c) Gọi I là giao BC và AD => AI là đường trung tuyến của tam giác ABC và AHD
Mà trọng tâm của tam giác ABC và AHD đều thuộc AI và thỏa mãn \(\frac{AG}{AI}=\frac{2}{3}\)
=> 2 tam giác này cùng trọng tâm


a) Ta có:
ˆABD=ˆCBD=\(\frac{\widehat{ABC}}{2}\)=120∘: 2=60∘
Từ A kẻ đường thẳng song song với BD cắt CD tại E.
Lại có:
ˆBAE=ˆABD=60∘(so le trong)
ˆCBD=ˆAEB=60∘ (đồng vị)
Suy ra tam giác ABE đều
⇒AB=BE=EA=6(cm)(1)
Khi đó: CE = BC + BE = 12 + 6 = 18 (cm)
Tam giác ACE có AE // BD nên suy ra:
\(\frac{BC}{CE}\)=\(\frac{DC}{AE}\)⇒BD=\(\frac{BC.AE}{CE}\)=\(\frac{12.6}{18}\)=4(cm)
b) Ta có:
MB=MC=\(\frac{1}{2}\).BC=\(\frac{1}{2}\).12=6(cm)(2)
Từ (1) và (2) suy ra:
BM=AB⇒BM=AB⇒ ∆ABM cân tại B.
Tam giác cân ABM có BD là đường phân giác nên đồng thời nó cũng là đường cao (tính chất tam giác cân). Vậy BD⊥AM
tk mik nha
C M B E D A
a) Ta có:
\(\widehat{ABD}=\widehat{CBD}=\frac{\widehat{ABC}}{2}=\frac{120^o}{2}=60^o\)
Từ A kẻ đường thẳng song song với BD cắt CB tại E
Lại có:
\(\widehat{BAE}=\widehat{ABD}=60^o\) ( so le trong )
\(\widehat{CBD}=\widehat{AEB}=60^o\) ( đồng vị )
Suy ra tam giác ABE đều
=> AB = BE = EA = 6 ( cm ) (1)
Khi đó: CE = BC + BE = 12 + 6 = 18 ( cm )
Tam giác ACE có AE // BD nên suy ra :
\(\frac{BC}{CE}=\frac{BD}{AE}\)
\(\Rightarrow BD=\frac{BC.AE}{CE}=\frac{12.6}{18}=4\left(cm\right)\)
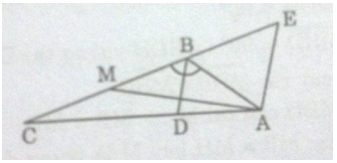
b) Ta có:
\(MB=MC=\frac{1}{2}.BC=\frac{1}{2}.12=6\left(cm\right)\left(2\right)\)
Từ (1) và (2) suy ra:
BM = AB => Tam giác ABM cân tại B.
Tam giác cân ABM có BD là đường phân giác nên đồng thời nó cũng là đường cao ( tính chất tam giác cân )
Vậy \(BD\perp AM\)

A B C D E x y
a) Xét tứ giác BEDC có:
\(\widehat{BEC}=\widehat{BDC}\)
\(\widehat{BEC}\)và \(\widehat{BDC}\) cùng nhìn cạnh BC
=> BEDC là tứ giác nội tiếp
b) Do BEDC là tứ giác nội tiếp nên: \(\widehat{BED}+\widehat{BCD}=180^o\)
Mà \(\widehat{BED}+\widehat{DEA}=180^o\Rightarrow\widehat{BCD}=\widehat{DEA}\)(*)
Mặt khác ta có:
\(\widehat{xAB}=\widehat{ACB}\)(cùng chắn cung AB)
hay \(\widehat{xAE}=\widehat{BCD}\)(**)
Từ (*) và (**) suy ra \(\widehat{DEA}=\widehat{xAE}\)
=> xy song song với ED (2 góc sole trong) (đpcm)
c) Do tứ giác BEDC là tứ giác nội tiếp
Mà \(\widehat{EBD}\)và \(\widehat{ECD}\)cùng nhìn cạnh ED
=> \(\widehat{EBD}=\widehat{ECD}\)(đpcm)
d) \(\widehat{BOC}=2\widehat{BAC}=120^o\)
DIện tích hình quạt BOC là: \(S_{qBOC}=\frac{\pi.R.n}{180}=\frac{\pi.2.120}{180}=\frac{4}{3}\pi\left(cm^2\right)\)
\(BC^2=OB^2+OC^2-2.OB.OC.cos120^o=12\Rightarrow BC=2\sqrt{3}\)
OH là đường cao, tam giác BOC cân tại O => BH=1/2.BC=\(\sqrt{3}\left(cm\right)\)
\(OH^2=OB^2-BH^2=2^2-3=1\Rightarrow OH=1\left(cm\right)\)
Diện tích tam giác BOC là: \(S_{\Delta BOC}=\frac{1}{2}.OH.BC=\frac{1}{2}.1.2\sqrt{3}=\sqrt{3}\left(cm^2\right)\)
=> Diện tích hình viên phân là: \(S_{vp}=S_{qBOC}-S_{\Delta BOC}=\frac{4}{3}\pi-\sqrt{3}\left(cm^2\right)\)