Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

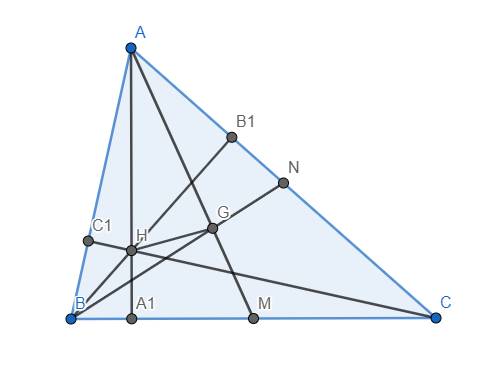
A B C A1 B1 C1 H x y z
Đặt AA1 = a , BB1 = b , CC1 = c , HA1 = x , HB1 = y , HC1 = z (với a,b,c,x,y,z > 0)
a) Đầu tiên , ta cần chứng minh : \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\) .
Thật vậy : \(\frac{x}{a}=\frac{x.BC}{a.BC}=\frac{S_{HBC}}{S_{ABC}}\); \(\frac{y}{b}=\frac{y.AC}{b.AC}=\frac{S_{AHC}}{S_{ABC}}\); \(\frac{z}{c}=\frac{z.AB}{c.AB}=\frac{S_{ABH}}{S_{ABC}}\)
\(\Rightarrow\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=\frac{S_{HBC}+S_{HAC}+S_{HAB}}{S_{ABC}}=\frac{S_{ABC}}{S_{ABC}}=1\)
Ta có : \(\frac{AA_1}{HA_1}+\frac{BB_1}{HB_1}+\frac{CC_1}{HC_1}=\left(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\right).1=\left(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\right).\left(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\right)\)
\(\ge\left(1+1+1\right)^2=9\)(áp dụng bđt Bunhiacopxki)
Vậy ta có đpcm
b) Ta có : \(\frac{HA_1}{HA}+\frac{HB_1}{HB}+\frac{HC_1}{HC}=\frac{x}{a-x}+\frac{y}{b-y}+\frac{z}{c-z}=\frac{1}{\frac{a}{x}-1}+\frac{1}{\frac{b}{y}-1}+\frac{1}{\frac{c}{z}-1}\)
Áp dụng bđt \(\frac{m^2}{i}+\frac{n^2}{j}+\frac{p^2}{k}\ge\frac{\left(m+n+p\right)^2}{i+j+k}\)(bạn tự chứng minh)
Ta có : \(\frac{1^2}{\frac{a}{x}-1}+\frac{1^2}{\frac{b}{y}-1}+\frac{1^2}{\frac{c}{z}-1}\ge\frac{\left(1+1+1\right)^2}{\left(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\right)-3}\ge\frac{9}{9-3}=\frac{3}{2}\)
(Từ câu a. ta có \(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\ge9\))
Vậy ta có đpcm

A B C D M N O I K P Q H S R L T E G
1) Do DN // AB nên ^DNC = ^BAC (Đồng vị). Mà ^BAC = ^DBC nên ^DNC = ^DBC => Tứ giác BNCD nội tiếp
Suy ra 5 điểm B,O,N,C,D cùng thuộc 1 đường tròn => ^BND = ^BOD = ^COD = ^CND
Ta có: DN // AB => ^BND = ^ABN. ^CND = ^NAB => ^NBA = ^NAB => \(\Delta\)ANB cân tại N (đpcm).
2) Ta có: ^DCM = ^DNB = ^DNC => \(\Delta\)DMC ~ \(\Delta\)DCN => DC2 = DM.DN. Dễ thấy: DC2 = DI.DA
Suy ra: DM.DN = DI.DA => Tứ giác AIMN nội tiếp => ^IMK = ^IAN = ^IBC => \(\Delta\)MIK ~ \(\Delta\)MKB (g.g)
=> KM2 = KI.KB. Ta lại có: ^KDI = ^IAB = ^KBD => \(\Delta\)IKD ~ \(\Delta\)DKB (g.g) => KD2 = KI.KB
Từ đó: KM2 = KD2 => KM = KD = DM/2. Do G là trung điểm KD nên \(\frac{GM}{GK}=3\) (1)
Gọi giao điểm của tia AD và tia ND là R. Theo hệ quả ĐL Thales: \(\frac{QB}{QM}=\frac{AB}{MR}\) (2)
Nếu ta gọi giao của PI với BC là V, theo phép vị tự thì I là trung điểm của PV. Từ đó suy ra: GM=GR
Mà GD = GK = GM/3 nên DK = MR/3. Lại áp dụng hệ quả ĐL Thales: \(\frac{IK}{IB}=\frac{DK}{AB}=\frac{MR}{3AB}\) (3)
Từ (1),(2),(3) suy ra: \(\frac{GM}{GK}.\frac{QB}{QM}.\frac{IK}{IB}=3.\frac{AB}{MR}.\frac{MR}{3AB}=1\). Theo đk đủ của ĐL Mélelaus thì 3 điểm Q,I,G tương ứng nằm trên các cạnh BM,BK,KM của \(\Delta\)BKM thẳng hàng (đpcm).
3) Gọi (HCS) cắt (O) tại điểm thứ hai là T. E là giao điểm của OD và BC.
Ta thấy: ^TBD = ^TCB = ^THS = ^THD (Góc tạo bởi tiếp tuyến và dây + Góc nội tiếp) => Tứ giác BHTD nội tiếp
Từ đó: 5 điểm B,H,E,T,D cùng thuộc 1 đường tròn => ^BTD = ^BED = 900
Mặt khác: ^DTE = 1800 - ^DBE = 1800 - ^BAC = ^BTC => ^DTE = ^BTC => ^BTD = ^CTE
Suy ra: ^CTE = 900 => T nằm trên đường tròn (CE) cố định. Mà T cũng thuộc (O) cố định.
Nên T là điểm cố định. Do đó: Dây CT của đường tròn (HCS) cố định
=> Tâm L của (HCS) luôn nằm trên đường trung trực của đoạn CT cố định (đpcm).
O A B C B1 A1 H K C1 M E N 1
a, Có : ^BCK = ^BAK ( chắn cung BK )
^BAK = ^BCH (Phụ ^ABC)
=> ^HCA1 = ^A1CK
=> CA1 là phân giác ^HCK
Tam giác HCK có CA1 vừa là đường cao vừa là phân giác
=> \(\Delta\)HCK cân tại C
=> CA1 là trung tuyến
=> A1 là trung điểm HK
b,\(\frac{HA}{AA_1}+\frac{HB}{BB_1}+\frac{HC}{CC_1}=1-\frac{HA_1}{AA_1}+1-\frac{HB_1}{BB_1}+1-\frac{HC_1}{CC_1}\)
\(=3-\frac{S_{BHC}}{S_{ABC}}-\frac{S_{AHC}}{S_{ABC}}-\frac{S_{AHB}}{S_{ABC}}\)
\(=3-1\)
\(=2\)
c,D \(OM\perp BC\)tại M nên M là trung điểm BC
Xét \(\Delta\)BB1C vuông tại B1 có B1M là trung tuyến
=> B1M = MB = MC
=> ^MBB1 = ^MB1B
và ^MB1C = ^MCB1
Mà ^B1AE = ^B1BC (Chắn cung EC)
^MB1C = ^AB1N (đối đỉnh)
^BB1M + ^CB1M = 90o
=> ^NAB1 + ^NB1A = 90o
=> \(B_1N\perp AE\)
Theo hệ thức lượng trong tam giác vuông có:
\(AB_1^2=AN.AE\)
\(EB_1^2=EN.EA\)
\(\Rightarrow\frac{AB_1^2}{EB_1^2}=\frac{AN.AE}{EN.EA}=\frac{AN}{EN}\)