Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cái hình thì mk gửi link trong ib nhé
a) Gọi O là giao điểm của AC và BD
\(\Delta OAB\) vuông tại O có \(OA^2+OB^2=AB^2=49\)
Lại có: \(\tan BAC=\tan OAB=\frac{OB}{OA}=\frac{3}{4}\)\(\Leftrightarrow\)\(\frac{OA^2}{16}=\frac{OB^2}{9}=\frac{OA^2+OB^2}{16+9}=\frac{49}{25}\)
\(\Rightarrow\)\(\hept{\begin{cases}\frac{OA}{4}=\frac{7}{5}\\\frac{OB}{3}=\frac{7}{5}\end{cases}}\Leftrightarrow\hept{\begin{cases}OA=\frac{28}{5}\left(cm\right)\\OB=\frac{21}{5}\left(cm\right)\end{cases}}\)
\(\Rightarrow\)\(\hept{\begin{cases}AC=2OA=\frac{56}{5}\left(cm\right)\\BD=2OB=\frac{42}{5}\left(cm\right)\end{cases}}\)
\(\Rightarrow\)\(S_{ABCD}=\frac{1}{2}AC.BD=\frac{1}{2}.\frac{56}{5}.\frac{42}{5}=\frac{1176}{25}=47,04\left(cm^2\right)\)
b) Gọi E, F lần lược là giao điểm của BD với MN và PQ
tam giác ABD có MQ // BD
\(\Rightarrow\)\(\frac{MQ}{BD}=\frac{MA}{AB}\) ( hệ quả định lí Talet )
tam giác OAD có QF // OA
\(\Rightarrow\)\(\frac{QF}{OA}=\frac{DQ}{AQ}=\frac{MB}{AB}\) ( hệ quả định lí Talet )
\(\Rightarrow\)\(\frac{MQ}{BD}+\frac{QF}{OA}=\frac{MA+MB}{AB}=1\)
\(\Rightarrow\)\(1\ge2\sqrt{\frac{MQ.QF}{BD.OA}}\)\(\Leftrightarrow\)\(MQ.QF\le\frac{1}{4}BD.OA\)
Tương tự, ta cũng có: \(NP.PF\le\frac{1}{4}BD.OC\)
\(\Rightarrow\)\(MQ.QF+NP.PF=S_{MEFQ}+S_{NEFP}=S_{MNPQ}\le\frac{1}{4}BD.AC=\frac{1}{2}S_{ABCD}=23,52\left(cm^2\right)\)
Dấu "=" xảy ra khi M, N, P, Q là trung điểm của AB, BC, CD, DA

1: Xét tứ giác APMQ có góc APM+góc AQM=180 độ
nên APMQ là tứ giác nội tiếp(1)
Xét tứ giác AHMP có góc AHM+góc APM=180 độ
nên AHMP là tứ giác nội tiếp(2)
Từ (1), (2) suy ra A,P,M,Q,H cùng thuộc 1 đường tròn
2:
Sửa đề: OH vuông góc với PQ
Xét (O) có
góc PAQ là góc nội tiếp chắn cung PQ
nên góc PAQ=1/2*góc POQ
=>góc POQ=120 độ
=>góc POH=góc QOH=60 độ
=>ΔPOH đều, ΔHOQ đều
=>OH là phân giác
=>OH vuông góc với PQ
=>OP=OH=PH=OQ=QH
=>OPHQ là hình thoi

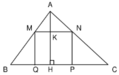
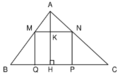
Vì ∆ ABC đồng dạng với ∆ AMN nên:
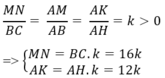
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
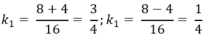
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
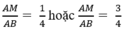

Vì ∆ ABC đồng dạng với ∆ AMN nên:
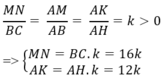
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
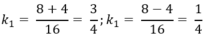
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
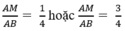
vào câu hỏi tương tự
Bui Duc Viet tham khảo nhé
Gọi diện tích h.c.n MNPQ là S1, diện tích tam giác ABC là S2=a
Ta có S1/S2 = PQ.QM//AH.BC (*)
Do PQ//BC => PQ/BC=AQ/AB
Do QM//AH => QM/AH=BQ/AB
(*) => S1/S2 = AQ.BQ/AB^2
=> S1=a.AQ.BQ/AB^2
=> S1 lớn nhất khi AQ.BQ lớn nhất
Ta có AQ.BQ<= [(AQ+BQ)/2]^2=(AB/2)^2
AQ.BQ lớn nhất khi AQ=BQ
=> Diện tích hình chữ nhật MNPQ có giá trị lớn nhất khi PQ đi qua trung điểm của đường cao AH.