Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có AB và AC cắt nhau tại A nên tọa độ A là nghiệm hệ:
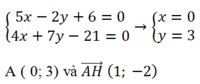
Ta có BH và AC vuông góc với nhau mà BH đi qua H (1;1) nên phương trình BH:
7(x-1) – 4( y-1) =0
Hay BH: 7x -4y – 3= 0
Có AB và BH cắt nhau tại B nên B( - 5; - 19/2 )
Phương trình BC nhận ![]() là VTPT và qua B
là VTPT và qua B
Suy r a (BC) : 1( x + 5) – 2( y+ 19/2) = 0 hay x- 2y -14 = 0

Đáp án :D
+Ta có hai đường thẳng AB và AC cắt nhau tại A nên tọa độ điểm A là nghiệm hệ phương trình:
5 x - 2 y + 6 = 0 4 x + 7 y - 21 = 0 → A ( 0 ; 3 ) v à A H → ( 1 ; - 2 )
+Ta có BH vuông góc với AC nên đường thẳng BH qua H(1;1) và nhận vecto u → ( 4 ; 7 ) làm VTCP và u → ( 7 ; - 4 ) làm VTPT
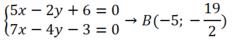
Suy ra phương trình đường thẳng BH là:
7( x-1) – 4( y-1) =0
=> 7x- 4y -3= 0
+ ta có AB và BH cắt nhau tại B nên tọa độ điểm B là nghiệm hệ phương trình:
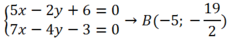
+Phương trình BC nhận A H → ( 1 ; - 2 ) là VTPT và qua B ( - 5 ; - 19 2 )
Suy ra phương trình (BC) :
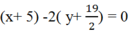
Hay x-2y-14= 0 .

Giả sử phương trình AC là 2x-5y+6=0 và pt BC là 4x+7y-21=0
Phương trình đường cao AH qua H và vuông góc BC:
\(7\left(x-0\right)-4\left(y-0\right)=0\Leftrightarrow7x-4y=0\)
Pt đường cao BH qua H vuông AB: \(2x+5y=0\)
Tọa độ A là nghiệm: \(\left\{{}\begin{matrix}2x-5y+6=0\\7x-4y=0\end{matrix}\right.\) \(\Leftrightarrow A\left(-4;-7\right)\)
Tọa độ B là nghiệm \(\left\{{}\begin{matrix}4x+7y-21=0\\2x+5y=0\end{matrix}\right.\) \(\Rightarrow B\left(\dfrac{35}{2};-7\right)\)
Phương trình AB: \(y+7=0\)

Trực tâm H là giao điểm của BH và AH ⇒ tọa độ H là nghiệm của hệ:
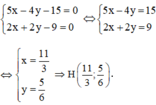
A là giao điểm của AB và AH nên tọa độ A là nghiệm của hệ phương trình:
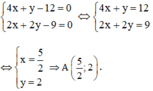
B là giao điểm BH và AB nên tọa độ điểm B là nghiệm của hệ:
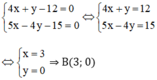
+ AC ⊥ HB, mà HB có một vtpt là (5; -4)⇒ AC nhận (4; 5) là một vtpt
AC đi qua 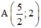
⇒ Phương trình đường thẳng AC: 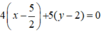 hay 4x + 5y – 20 = 0.
hay 4x + 5y – 20 = 0.
+ CH ⊥ AB, AB có một vtpt là (4; 1) ⇒ CH nhận (1; -4) là một vtpt
CH đi qua 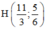
⇒ Phương trình đường thẳng CH: 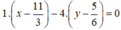 hay CH: 3x – 12y - 1 = 0.
hay CH: 3x – 12y - 1 = 0.
+ BC ⊥ AH , mà AH nhận (2; 2) là một vtpt
⇒ BC nhận (1; -1) là một vtpt
BC đi qua B(3; 0)
⇒ Phương trình đường thẳng BC: 1(x - 3) – 1(y – 0) = 0 hay x – y – 3 = 0.

Tọa độ A là nghiệm: \(\left\{{}\begin{matrix}x-y-2=0\\x+2y-5=0\end{matrix}\right.\) \(\Rightarrow A\left(3;1\right)\)
\(\left\{{}\begin{matrix}x_A+x_B+x_C=3x_G\\y_A+y_B+y_C=3y_G\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_B+x_C=6\\y_B+y_C=5\end{matrix}\right.\) (1)
B thuộc AB nên: \(x_B-y_B=2\Rightarrow x_B=y_B+2\)
C thuộc AC nên: \(x_C+2y_C-5=0\Rightarrow x_C=-2y_C+5\)
Thế vào (1) \(\Rightarrow\left\{{}\begin{matrix}y_B+2-2y_C+5=6\\y_B+y_C=5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}y_B=3\Rightarrow x_B=5\\y_C=2\Rightarrow x_C=1\end{matrix}\right.\)
Phương trình BC: \(\dfrac{x-5}{1-5}=\dfrac{y-3}{2-3}\Leftrightarrow x-4y+7=0\)

A B C P(1,2;5,6)
Điểm P có tọa độ \(\left(\frac{5}{6};\frac{28}{5}\right)\). Đặt \(\widehat{ABC}=\alpha\). Do tam giác ABC cân tại A nên \(\alpha\in\left(0;\frac{\pi}{2}\right)\) do đó \(\alpha=\left(\widehat{AB,BC}\right)=\left(\widehat{BC,CA}\right)\)
và \(\cos\alpha=\frac{\left|4.1+\left(-1\right).\left(-2\right)\right|}{\sqrt{4^2+\left(-1\right)^2}.\sqrt{1^2+\left(-2\right)^2}}=\frac{6}{\sqrt{5.17}}\)
Do đó bài toán trở thành viết phương trình đường thẳng đi qua \(P\left(\frac{6}{5};\frac{28}{7}\right)\) không song song với AB, tạo với BC góc \(\alpha\) mà \(\cos\alpha=\frac{6}{\sqrt{5.17}}\) (1)
Đường thẳng AC cần tìm có vecto pháp tuyến \(\overrightarrow{n}=\left(a;b\right)\) với \(a^2+b^2\ne0\) và \(a\ne-4b\) (do AC không cùng phương với AB). Từ đó và (1) suy ra :
\(\frac{6}{\sqrt{5.17}}=\frac{\left|a-2b\right|}{\sqrt{5}.\sqrt{a^2+b^2}}\Leftrightarrow6\sqrt{a^2+b^2}=\sqrt{17}.\left|a-2b\right|\)
\(\Leftrightarrow19a^2+68ab-32b^2=0\)
\(\Leftrightarrow\left(a+4b\right)\left(19a-8b\right)=0\)
\(\Leftrightarrow19a=8b\) (do \(a\ne-4b\) (2)
Từ (2) và do \(a^2+b^2\ne0\), chọn a=40, b=95 được phương trình đường thẳng AC cần tìm là \(40\left(x-\frac{6}{5}\right)+95\left(y-\frac{28}{5}\right)=0\) hay \(8x+19y-116=0\)


- toạ độ điểm A(0,3) => vecto ah (1;-2)
mà vecto ah vuông góc vecto bc => vecto chỉ phương ah = vecto pháp tuyến bc = (1;-2)
B thuộc AB => 5xb - 2yb = -6
C thuộc AC => 4xc + 7yc = 21
xc - xb = 1
yc - yb = -2
giải hệ 4 pt => toạ độ điểm B, C
- Có vecto pháp tuyến, điểm B(C) => viết phương trình đường thẳng