Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C x y
Giải:
a) Ta có: \(\widehat{B}+\widehat{C}=\widehat{Cax}\)
Mà \(\widehat{B}=\widehat{C}\) ( t/g ABC cân tại A )
\(\Rightarrow2\widehat{B}=\widehat{Cax}\) ( đpcm )
\(\Rightarrow\widehat{B}=\frac{1}{2}\widehat{xAC}\)
b) Ta có: \(\widehat{xAy}=\widehat{yAC}=\frac{1}{2}\widehat{xAC}\)
Mà \(\widehat{B}=\frac{1}{2}\widehat{xAC}\)
\(\Rightarrow\widehat{B}=\widehat{xAy}\left(đpcm\right)\)
c) Vì \(\widehat{B}=\widehat{yAC}\) mà 2 góc này ở vị trí so le trong nên Ay // BC ( đpcm )
Vậy...

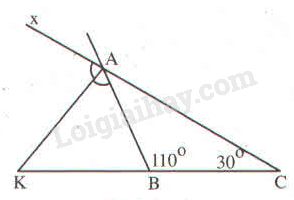
Ta có \(\widehat{xAB}\) là góc ngoài tại đỉnh A của \(\Delta ABC.\)
\(\Rightarrow\widehat{xAB}=\widehat{ABC}+\widehat{ACB}\) (tính chất góc ngoài tam giác).
\(\Rightarrow\widehat{xAB}=110^0+30^0\)
\(\Rightarrow\widehat{xAB}=140^0.\)
Vì \(AK\) là tia phân giác của \(\widehat{BAx}\left(gt\right)\)
\(\Rightarrow\widehat{xAK}=\widehat{KAB}=\frac{\widehat{BAx}}{2}=\frac{140^0}{2}=70^0\) (1)
Lại có: \(\widehat{ABC}+\widehat{ABK}=180^0\) (vì 2 góc kề bù)
\(\Rightarrow110^0+\widehat{ABK}=180^0\)
\(\Rightarrow\widehat{ABK}=180^0-110^0\)
\(\Rightarrow\widehat{ABK}=70^0\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{KAB}=\widehat{ABK}=70^0.\)
Mà 2 góc này thuộc \(\Delta KAB\)
\(\Rightarrow\Delta KAB\) có 2 góc bằng nhau (đpcm).
Chúc bạn học tốt!

Bài 3:
Xét 2 \(\Delta\) \(AMO\) và \(BNO\) có:
\(\widehat{MAO}=\widehat{NBO}=90^0\left(gt\right)\)
\(OA=OB\) (vì O là trung điểm của \(AB\))
\(AM=BN\left(gt\right)\)
=> \(\Delta AMO=\Delta BNO\left(c-g-c\right)\)
=> \(\widehat{MOA}=\widehat{NOB}\) (2 góc tương ứng)
Mà \(\widehat{MOA}+\widehat{MOB}=180^0\) (vì 2 góc kề bù)
=> \(\widehat{NOB}+\widehat{MOB}=180^0.\)
=> \(M,O,N\) thẳng hàng. (1)
Ta có: \(\Delta AMO=\Delta BNO\left(cmt\right)\)
=> \(OM=ON\) (2 cạnh tương ứng) (2)
Từ (1) và (2) => \(O\) là trung điểm của \(MN\left(đpcm\right).\)
Bài 4:
Chúc bạn học tốt!