Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

uiuukngkgkinbjkmjbkndojkjzzzzzzznvnnhchnckckbhhoihvkjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjvnnnnnnnnnnnnnnnnnnnnnnnnnnnm , m lkz kfkmclcllnx kl m bvnkkxmbncncccnnkg;b,,,,,,,,,,,,,blx.x,yl kb,b.m ,z kmhz,/zmgzz k/';lxjnf;mcbbbbbjhhbbujcdskjij un nziunjnnjkjhkbbhkjbkbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbxjxnk,k,fzknkb,

ta có AB=AM+MB=11+8=19 (cm)
xát tgAMN và tgABC có gA chung
gAMN = gABC (hai góc đồng vị của MN//BC)
=>tgAMN ~ tgABC (g.g)
=>AM/AB=AN/AC=>11/19=AN/38
=>AN=22 (cm)
ta có AC=AN+NC=>NC = 38-22=16(cm)

Vì tam giác ABC cân tại A nên AB = AC = 10cm
Vì MN// BC, theo định lí Ta – let ta có:
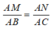
Mà AB = AC nên AM = AN = 4cm
Suy ra :

Chọn đáp án C

Bài 3. Cho tam giác
ABC
. Trên cạnh
AC
lấy điểm
N
sao cho
2
5
CN
AN
. Trên cạnh BC lấy điểm
M
sao cho
BC xMC
và MN // AB.
Tìm x.
A. 5 B. 2,5 C. 3,5 D. 1,4


a
Do \(MN//BC\) nên theo định lý Thales ta có:\(\frac{AN}{NC}=\frac{AM}{MB}=\frac{MN}{BC}\)
\(\Rightarrow\frac{8}{NC}=\frac{3}{2}\Rightarrow NC=\frac{16}{3}\)
Áp dụng định Pythagoras ta có:\(AM^2+AN^2=MN^2\Rightarrow MN=\sqrt{AM^2+AN^2}=10\)
Mà \(\frac{AM}{MB}=\frac{MN}{BC}\Rightarrow\frac{3}{2}=\frac{10}{BC}\Rightarrow BC=\frac{20}{3}\)
b
Hạ \(NH\perp BC;MG\perp BC\)
Áp dụng định lý Pythagoras vào tam giác ABC ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AB^2=\sqrt{BC^2-AC^2}\Rightarrow AB=\sqrt{10-\left(\frac{16}{3}\right)^2-8^2}=\frac{2\sqrt{17}}{3}\)
Bạn áp dụng định lý Ta Lét ( do ND//AB ) rồi tính được ND
Diện tích tam giác vuông NCD sẽ tính bằng \(\frac{NC\cdot ND}{2}\) ( do đã biết được ND và NC )
Lại có \(S_{NCD}=\frac{NH\cdot CD}{2}\) rồi tính được NH.
Do NH=MG nên tính được diện tích hình bình hành BMND.Hướng là thế đấy,bạn làm tiếp nha,mik nhác quá:(

a: AN+CN=AC
=>AN=20-15=5cm
Xét ΔABC có AM/AB=AN/AC
nên MN//BC
b: Xét ΔAMN và ΔNPC có
góc AMN=góc NPC(=góc B)
góc ANM=góc NCP
=>ΔAMN đồng dạng với ΔNPC

Xét ΔABC có MN//BC
nên AM/AB=AN/AC
=>AN/20=4/20=1/5
nên AN=4(cm)
Xét tam giác ABC và MN//BC
Hai tam giác AMN và ABC, có:
- góc AMN = góc ABC (đồng vị)
- góc ANM = góc ACB (đồng vị)
- BAC là góc chung
Mặt khác, theo hệ quả định lí Ta-lét, hai tam giác AMN và ABC có 3 cặp cạnh tương ứng tỉ lệ:
\(\frac{AM}{AB}=\frac{MN}{BC}=\frac{AN}{AC}\)
Nên tam giác AMN đồng dạng với tam giác ABC
\(\Rightarrow\frac{AM}{AB}=\frac{AN}{AC}=\frac{1}{3}\)
\(\Rightarrow\frac{AN}{18}=\frac{1}{3}\)
\(AN=\frac{18.1}{3}=6\)
Do AC = AN + NC
\(\Rightarrow NC=AC-AN=18-6=12\)
Vậy NC có độ dài là 12 cm